
【題目】已知O為直線AB上一點,射線OD、OC、OE位于直線AB上方,OD在OE的左側,∠AOC=120°,∠DOE=50°,設∠BOE=![]()
(1)若射線OE在∠BOC的內部(如圖所示):
①若![]() =43°,求∠COD的度數;
=43°,求∠COD的度數;
②當∠AOD=3∠COE時,求∠COD的度數;
(2)若射線OE恰為圖中某一個角(小于180°)的角平分線,試求![]() 的值.
的值.

【答案】(1)①33°②15°
(2)n的值為30°或50°或110°或120°
【解析】
(1)①根據已知條件,可先求出∠COE,再根據角的差求出∠COD
②分兩種情況討論:當OD在∠BOC之間時;OD在∠AOC內的情況
(2)分四種情況討論:當OE分別是∠BOC、∠BOD、∠COD、∠COA的角平分線時,根據角平分線的性質分別求出即可
(1)①∵∠BOC=180°∠AOC,∠AOC=120°
∴∠BOC=180°120°=60°
∵∠COE=∠BOC∠BOE,∠BOE=n=43°
∠COD=∠DOE∠COE,∠DOE=50°
∴∠COD=50°(60°43°)=33°
②當∠DOE在∠BOC之間時,設∠COD=x,則由題意可得:120+x=3(50+x)無解;
當OD在∠AOC之間時,設∠COD=x,則由題意可得120-x=3(50-x)解得x=15°
所以當∠AOD=3∠COE時,∠COD=15°
(2)如圖: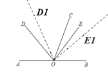
當OE1平分∠BOC時,
∵∠AOC=120°
∴∠BOC=180°120°=60°
∴n=∠BOE1= ∠BOC=30°;
如圖: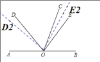
當OE2平分∠BOD2時,
n=∠BOE2=∠D2OE=50°;
如圖: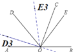
當OE3平分∠COD3時,
∵∠E3OC=∠D3OE3=50°,∠BOC=180°∠AOC=180°120°=60°
∴n=∠BOE3=∠BOC+∠E3OC=60°+50°=110°;
如圖: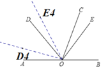
當OE4平分∠AOC時,
∵∠COE4= ∠AOC= ×120°=60°
∠BOC=180°∠AOC=180°120°=60°
∴n=∠BOE4=∠BOC+∠COE4=60°+60°=120°


科目:初中數學 來源: 題型:
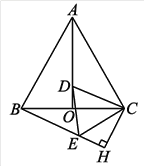
【題目】在等邊△ABC中,AO是高,D為AO上一點,以CD為一邊,在CD下方作等邊△CDE,連接BE.
(1)求證:AD=BE;
(2)過點C作CH⊥BE,交BE的延長線于H,若BC=8,求CH的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校八年級(1)班為了了解同學們一天零花錢的消費情況,對本班同學開展了調查,將同學一周的零花錢以2元為組距,繪制如圖的頻率分布直方圖,已知從左到右各組的頻數之比為2∶3∶4∶2∶1.

(1)若該班有48人,則零花錢用最多的是第_____組,有_______人;
(2)零花錢在8元以上的共有_____人;
(3)若每組的平均消費按最大值計算,則該班同學的日平均消費額是_______元(精確到0.1元)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料
小明遇到這樣一個問題:求計算![]() 所得多項式的一次項系數.
所得多項式的一次項系數.
小明想通過計算![]() 所得的多項式解決上面的問題,但感覺有些繁瑣,他想探尋一下,是否有相對簡潔的方法.
所得的多項式解決上面的問題,但感覺有些繁瑣,他想探尋一下,是否有相對簡潔的方法.
他決定從簡單情況開始,先找![]() 所得多項式中的一次項系數.通過觀察發現:
所得多項式中的一次項系數.通過觀察發現:
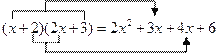
也就是說,只需用![]() 中的一次項系數1乘以
中的一次項系數1乘以![]() 中的常數項3,再用
中的常數項3,再用![]() 中的常數項2乘以
中的常數項2乘以![]() 中的一次項系數2,兩個積相加
中的一次項系數2,兩個積相加![]() ,即可得到一次項系數.
,即可得到一次項系數.
延續上面的方法,求計算![]() 所得多項式的一次項系數.可以先用
所得多項式的一次項系數.可以先用![]() 的一次項系數1,
的一次項系數1, ![]() 的常數項3,
的常數項3, ![]() 的常數項4,相乘得到12;再用
的常數項4,相乘得到12;再用![]() 的一次項系數2,
的一次項系數2, ![]() 的常數項2,
的常數項2, ![]() 的常數項4,相乘得到16;然后用
的常數項4,相乘得到16;然后用![]() 的一次項系數3,
的一次項系數3, ![]() 的常數項2,
的常數項2, ![]() 的常數項3,相乘得到18.最后將12,16,18相加,得到的一次項系數為46.
的常數項3,相乘得到18.最后將12,16,18相加,得到的一次項系數為46.
參考小明思考問題的方法,解決下列問題:
(1)計算![]() 所得多項式的一次項系數為 .
所得多項式的一次項系數為 .
(2)計算![]() 所得多項式的一次項系數為 .
所得多項式的一次項系數為 .
(3)若計算![]() 所得多項式的一次項系數為0,則
所得多項式的一次項系數為0,則![]() =_________.
=_________.
(4)若![]() 是
是![]() 的一個因式,則
的一個因式,則![]() 的值為 .
的值為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有個均勻的正十二面體的骰子,其中1個面標有“1”,2個面標有“2”,3個面標有“3”,2個面標有“4”,1個面標有“5”,其余面標有“6”,將這個骰子擲出后:
(1)擲出“6”朝上的可能性有多大?
(2)哪些數字朝上的可能性一樣大?
(3)哪些數字朝上的可能性最大?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】初二年級教師對試卷講評課中學生參與情況進行調查,調查項目分為主動質疑、獨立思考、專注聽講、講解題目四項.調查組隨機抽取了若干名初中學生的參與情況,繪制了如圖所示的扇形統計圖和條形統計圖(均不完整),請根據圖中所給信息解答下列問題:

(1)在扇形統計圖中,項目“主動質疑”所在的扇形的圓心角的度數為______度;
(2)請將頻數分布直方圖補充完整;
(3)如果全市有6000名初三學生,那么在試卷評講課中,“獨立思考”的初二學生約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某收費站在2小時內對經過該站的機動車統計如下:
類型 | 轎車 | 貨車 | 客車 | 其他 |
數量(輛) | 36 | 24 | 8 | 12 |
若有一輛機動車將經過這個收費站,利用上面的統計估計它是轎車的概率為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了增強中學生的體質,某校食堂每天都為學生提供一定數量的水果,學校李老師為了了解學生喜歡吃哪種水果,進行了抽樣調查,調查分為五種類型:A喜歡吃蘋果的學生;B喜歡吃桔子的學生;C.喜歡吃梨的學生;D.喜歡吃香蕉的學生;E喜歡吃西瓜的學生,并將調查結果繪制成圖1和圖2 的統計圖(不完整).請根據圖中提供的數據解答下列問題: 
(1)求此次抽查的學生人數;
(2)將圖2補充完整,并求圖1中的x;
(3)現有5名學生,其中A類型3名,B類型2名,從中任選2名學生參加體能測試,求這兩名學生為同一類型的概率(用列表法或樹狀圖法)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com