
【題目】已知:![]() ,
,![]() .
.
(1)當![]() >0時,判斷
>0時,判斷![]() 與0的關系,并說明理由;
與0的關系,并說明理由;
(2)設![]() .
.
①當![]() 時,求
時,求![]() 的值;
的值;
②若![]() 是整數,求
是整數,求![]() 的正整數值.
的正整數值.
【答案】(1)見解析;(2)①1;②4或3或1
【解析】
(1)作差后,根據分式方程的加減法法則計算即可;
(2)①把M、N代入整理得到y,解分式方程即可;
②把y變形為:![]() ,由于x為整數,y為整數,則
,由于x為整數,y為整數,則![]() 可以取±1,±2,然后一一檢驗即可.
可以取±1,±2,然后一一檢驗即可.
(1)當![]() 時,M-N≥0.理由如下:
時,M-N≥0.理由如下:
M-N=![]() .
.
∵![]() >0,∴(x-1)2≥0,2(x+1)>0,∴
>0,∴(x-1)2≥0,2(x+1)>0,∴![]() ,∴M-N≥0.
,∴M-N≥0.
(2)依題意,得:![]() .
.
①當![]() ,即
,即![]() 時,解得:
時,解得:![]() .經檢驗,
.經檢驗,![]() 是原分式方程的解,∴當y=3時,x的值是1.
是原分式方程的解,∴當y=3時,x的值是1.
②![]() .
.
∵![]() 是整數,∴
是整數,∴![]() 是整數,∴
是整數,∴![]() 可以取±1,±2.
可以取±1,±2.
當x+1=1,即![]() 時,
時,![]() ;
;
當x+1=﹣1時,即![]() 時,
時,![]() (舍去);
(舍去);
當x+1=2時,即![]() 時,
時,![]() ;
;
當x+1=-2時,即![]() 時,
時,![]() ;
;
綜上所述:當![]() 為整數時,
為整數時,![]() 的正整數值是4或3或1.
的正整數值是4或3或1.


 優質課堂快樂成長系列答案
優質課堂快樂成長系列答案科目:初中數學 來源: 題型:
【題目】如圖,等腰梯形ABCD中,AB∥CD,AB=2CD,AC交BD于點O,點E、F分別為AO、BO的中點,則下列關于點O成中心對稱的一組三角形是( )
A.△ABO與△CDO
B.△AOD與△BOC
C.△CDO與△EFO
D.△ACD與△BCD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了加強對校內外安全監控,創建平安校園,某學校計劃增加15臺監控攝像設備,現有甲、乙兩種型號的設備,其中每臺價格,有效監控半徑如表所示,經調查,購買1臺甲型設備比購買1臺乙型設備多150元,購買2臺甲型設備比購買3臺乙型設備少400元.
甲型 | 乙型 | |
價格(元/臺) | a | b |
有效半徑(米/臺) | 150 | 100 |
(1)求a、b的值;
(2)若購買該批設備的資金不超過11000元,且要求監控半徑覆蓋范圍不低于1600米,兩種型號的設備均要至少買一臺,請你為學校設計購買方案,并計算最低購買費用.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】教材在探索平方差公式時利用了面積法,面積法除了可以幫助我們記憶公式,還可以直觀地推導或驗證公式,俗稱“無字證明”,例如,著名的趙爽弦圖(如圖①,其中四個直角三角形較大的直角邊長都為![]() ,較小的直角邊長都為
,較小的直角邊長都為![]() ,斜邊長都為
,斜邊長都為![]() ),大正方形的面積可以表示為
),大正方形的面積可以表示為![]() ,也可以表示為
,也可以表示為![]() ,由此推導出重要的勾股定理:如果直角三角形兩條直角邊長為
,由此推導出重要的勾股定理:如果直角三角形兩條直角邊長為![]() ,斜邊長為
,斜邊長為![]() ,則
,則![]() .
.
(1)圖②為美國第二十任總統伽菲爾德的“總統證法”,請你利用圖②推導勾股定理.
(2)如圖③,在![]() 中,
中,![]() 是
是![]() 邊上的高,
邊上的高,![]() ,
,![]() ,
,![]() ,設
,設![]() ,求
,求![]() 的值.
的值.
(3)試構造一個圖形,使它的面積能夠解釋![]() ,畫在如圖4的網格中,并標出字母
,畫在如圖4的網格中,并標出字母![]() 所表示的線段.
所表示的線段.

查看答案和解析>>
科目:初中數學 來源: 題型:
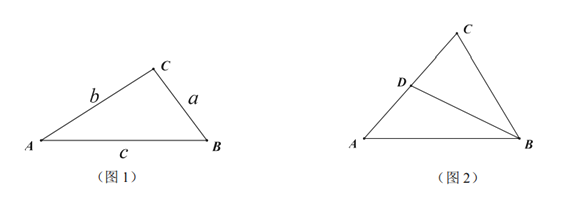
【題目】如圖1,![]() 的
的![]() 所對邊分別是
所對邊分別是![]() ,且
,且![]() ,若滿足
,若滿足![]() ,則稱
,則稱![]() 為奇異三角形,例如等邊三角形就是奇異三角形.
為奇異三角形,例如等邊三角形就是奇異三角形.
(1)若![]() ,判斷
,判斷![]() 是否為奇異三角形,并說明理由;
是否為奇異三角形,并說明理由;
(2)若![]() ,
,![]() ,求
,求![]() 的長;
的長;
(3)如圖2,在奇異三角形![]() 中,
中,![]() ,點
,點![]() 是
是![]() 邊上的中點,連結
邊上的中點,連結![]() ,
,![]() 將
將![]() 分割成2個三角形,其中
分割成2個三角形,其中![]() 是奇異三角形,
是奇異三角形,![]() 是以
是以![]() 為底的等腰三角形,求
為底的等腰三角形,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列一組圖形中點的個數,其中第1個圖中共有4個點,第2個圖中共有10個點,第3個圖中共有19個點,…,按此規律第100個圖中共有點的個數是

A. 15151B. 15152C. 15153D. 15154
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】完成下面的證明:
已知:如圖,AB∥DE,求證:∠D+∠BCD﹣∠B=180°,
證明:過點C作CF∥AB.

∵AB∥CF(已知),
∴∠B= ( ).
∵AB∥DE,CF∥AB( 已知 ),
∴CF∥DE ( )
∴∠2+ =180° ( )
∵∠2=∠BCD﹣∠1,
∴∠D+∠BCD﹣∠B=180° ( ).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com