
【題目】完全平方公式:(a±b)2=a2±2ab+b2適當的變形,可以解決很多的數學問題.
例如:若a+b=3,ab=1,求a2+b2的值.
解:因為a+b=3,ab=1
所以(a+b)2=9,2ab=2
所以a2+b2+2ab=9,2ab=2
得a2+b2=7
根據上面的解題思路與方法,解決下列問題:
(1)若(7﹣x)(x﹣4)=1,求(7﹣x)2+(x﹣4)2的值;
(2)如圖,點C是線段AB上的一點,以AC、BC為邊向兩邊作正方形,設AB=5,兩正方形的面積和S1+S2=17,求圖中陰影部分面積.

 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案 名校名師培優作業本加核心試卷系列答案
名校名師培優作業本加核心試卷系列答案科目:初中數學 來源: 題型:
【題目】如圖所示,在平面直角坐標系中,四邊形ABCD是直角梯形,BC∥AD,∠BAD=90°,BC與y軸相交于點M,且M是BC的中點,A,B,D三點的坐標分別是A(﹣1,0),B(﹣l,2),D(3,0).連接DM,并把線段DM沿DA方向平移到ON.若拋物線y=ax2+bx+c經過點D,M,N.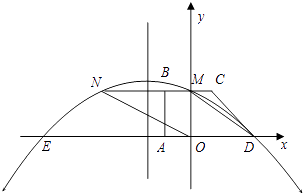
(1)求拋物線的解析式.
(2)拋物線上是否存在點P,使得PA=PC?若存在,求出點P的坐標;若不存在,請說明理由.
(3)設拋物線與x軸的另一個交點為E,點Q是拋物線的對稱軸上的一個動點,當點Q在什么位置時有|QE﹣QC|最大?并求出最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在扇形AOB中∠AOB=90°,正方形CDEF的頂點C是 ![]() 的中點,點D在OB上,點E在OB的延長線上,當正方形CDEF的邊長為2
的中點,點D在OB上,點E在OB的延長線上,當正方形CDEF的邊長為2 ![]() 時,則陰影部分的面積為( )
時,則陰影部分的面積為( )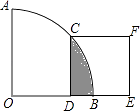
A.2π﹣4
B.4π﹣8
C.2π﹣8
D.4π﹣4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,∠ABC=60°,AB=2,點P是這個菱形內部或邊上的一點,若以點P,B,C為頂點的三角形是等腰三角形,則P,D(P,D兩點不重合)兩點間的最短距離為 . 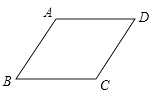
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,四邊形![]() 中,
中,![]() .
.
(1)動點![]() 從
從![]() 出發,以每秒1個單位的速度沿路線
出發,以每秒1個單位的速度沿路線![]() 運動到點
運動到點![]() 停止,設運動時間為
停止,設運動時間為![]() ,
,![]() 的面積為
的面積為![]() 關于
關于![]() 的函數圖象如圖②所示,求
的函數圖象如圖②所示,求![]() 的長.
的長.
(2)如圖③動點![]() 從點
從點![]() 出發,以每秒2個單位的速度沿路線
出發,以每秒2個單位的速度沿路線![]() 運動到點
運動到點![]() 停止,同時,動點
停止,同時,動點![]() 從點
從點![]() 出發,以每秒5個單位的速度沿路線
出發,以每秒5個單位的速度沿路線![]() 運動到點
運動到點![]() 停止,設運動時間為
停止,設運動時間為![]() ,當
,當![]() 點運動到
點運動到![]() 邊上時,連接
邊上時,連接![]() ,當
,當![]() 的面積為8時,求
的面積為8時,求![]() 的值.
的值.
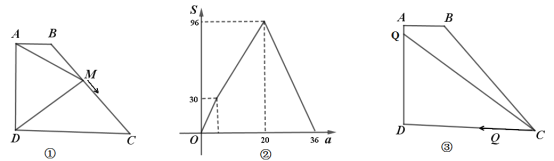
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)思考探究:如圖,△ABC的內角∠ABC的平分線與外角∠ACD的平分線相交于P點,已知∠ABC=70°,∠ACD=100°.求∠A和∠P的度數.
(2)類比探究:如圖,△ABC的內角∠ABC的平分線與外角∠ACD的平分線相交于P點,已知∠P=n°.求∠A的度數(用含n的式子表示).
(3)拓展遷移:已知,在四邊形ABCD中,四邊形ABCD的內角∠ABC與外角∠DCE的平分線所在直線相交于點P,∠P=n°,請畫出圖形;并探究出∠A+∠D的度數(用含n的式子表示).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某加工廠加工一批綠色蔬菜,若12個大加工車間和15個小加工車間一天同時加工,則可加工綠色蔬菜1575噸;若3個大加工車間和5個小加工車間一天同時加工,則可加工綠色蔬菜450噸.
(1)每個大車間和每個小車間每天各加工多少噸綠色蔬菜?
(2)若該工廠有25個大加工車間,20個小加工車間;每個大車間每天耗費3000元,每個小車間每天耗費2500元,現有2250噸綠色蔬菜,要求一天之內加工完,如何分配車間才能更省錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在正方形ABCD中,E,F分別是AD,CD上兩點,BE交AF于點G,且DE=CF.
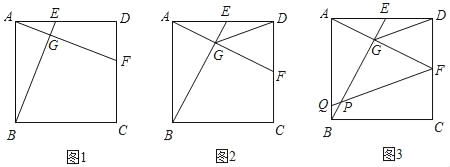
(1)寫出BE與AF之間的關系,并證明你的結論;
(2)如圖2,若AB=2,點E為AD的中點,連接GD,試證明GD是∠EGF的角平分線,并求出GD的長;
(3)如圖3,在(2)的條件下,作FQ∥DG交AB于點Q,請直接寫出FQ的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com