
【題目】如圖,在ABCD中,AE、BF分別平分∠DAB和∠ABC,交CD于點E、F,AE、BF相交于點M. 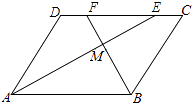
(1)試說明:AE⊥BF;
(2)判斷線段DF與CE的大小關系,并予以說明.
【答案】
(1)解:方法一:如圖①,
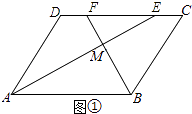
∵在ABCD中,AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE、BF分別平分∠DAB和∠ABC,
∴∠DAB=2∠BAE,∠ABC=2∠ABF
∴2∠BAE+2∠ABF=180°.
即∠BAE+∠ABF=90°.
∴∠AMB=90°.
∴AE⊥BF.
方法二:如圖②,延長BC、AE相交于點P,
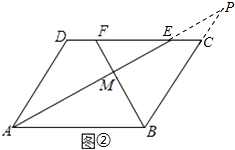
∵在ABCD中,AD∥BC,
∴∠DAP=∠APB.
∵AE平分∠DAB,
∴∠DAP=∠PAB.
∴∠APB=∠PAB.
∴AB=BP.
∵BF平分∠ABP,
∴AP⊥BF,
即AE⊥BF.
(2)解:方法一:線段DF與CE是相等關系,即DF=CE,
∵在ABCD中,CD∥AB,
∴∠DEA=∠EAB.
又∵AE平分∠DAB,
∴∠DAE=∠EAB.
∴∠DEA=∠DAE.
∴DE=AD.(6分)
同理可得,CF=BC.
又∵在ABCD中,AD=BC,
∴DE=CF.
∴DE﹣EF=CF﹣EF.
即DF=CE.
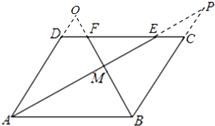
方法二:如圖,延長BC、AE設交于點P,延長AD、BF相交于點O,
∵在ABCD中,AD∥BC,
∴∠DAP=∠APB.
∵AE平分∠DAB,
∴∠DAP=∠PAB.
∴∠APB=∠PAB.
∴BP=AB.
同理可得,AO=AB.
∴AO=BP.
∵在ABCD中,AD=BC,
∴OD=PC.
又∵在ABCD中,DC∥AB,
∴△ODF∽△OAB,△PCE∽△PBA.
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() .
.
∴DF=CE.
【解析】(1)因為AE,BF分別是∠DAB,∠ABC的角平分線,那么就有∠MAB= ![]() ∠DAB,∠MBA=
∠DAB,∠MBA= ![]() ∠ABC,而∠DAB與∠ABC是同旁內角互補,所以,能得到∠MAB+∠MBA=90°,即得證.(2)兩條線段相等.利用平行四邊形的對邊平行,以及角平分線的性質,可以得到△ADE和△BCF都是等腰三角形,那么就有CF=BC=AD=DE,再利用等量減等量差相等,可證.
∠ABC,而∠DAB與∠ABC是同旁內角互補,所以,能得到∠MAB+∠MBA=90°,即得證.(2)兩條線段相等.利用平行四邊形的對邊平行,以及角平分線的性質,可以得到△ADE和△BCF都是等腰三角形,那么就有CF=BC=AD=DE,再利用等量減等量差相等,可證.


科目:初中數學 來源: 題型:
【題目】如圖1,點A,B,O,C為數軸上四點,點A對應數a(a<﹣2),點O對應0,點C對應3,AB=2 (AB表示點A到點B的距離).
(1)填空:點C到原點O的距離 ,:點B對應的數 .(用含有a的式子)
(2)如圖2,將一刻度尺放在數軸上,刻度尺上“6cm”和“8.7cm”分別對應數軸上的點O和點C,若BC=5,求a的值和點A在刻度尺上對應的刻度.
(3)如圖3,在(2)的條件下,點A以1單位長度/秒的逮度向右運動,同時點C向左運動,若運動3秒時,點A和點C到原點D的距離相等,求點C的運動速度.)
查看答案和解析>>
科目:初中數學 來源: 題型:
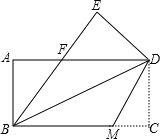
【題目】如圖,把一張矩形的紙ABCD沿對角線BD折疊,使點C落在點E處,BE與AD交于點F.
⑴求證:ΔABF≌ΔEDF;
⑵若將折疊的圖形恢復原狀,點F與BC邊上的點M正好重合,連接DM,試判斷四邊形BMDF的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,多邊形OABCDE的頂點坐標為O(0,0),A(2,0),B(2,2),C(4,2),D(4,4),E(0,4),若如圖過點M(1,2)的直線MP(與y軸交于點P)將多邊形OABCDE分割成面積相等的兩部分,則直線MP的函數表達式是 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
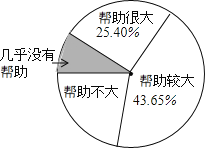
【題目】為了解“數學思想作文對學習數學幫助有多大?”一研究員隨機抽取了一定數量的高校大一學生進行了問卷調查,并將調查得到的數據用下面的扇形圖和表來表示(圖、表都沒制作完成).
選項 | 幫助很大 | 幫助較大 | 幫助不大 | 幾乎沒有幫助 |
人數 | a | 543 | 269 | b |
根據圖、表提供的信息.
(1)請問:這次共有多少名學生參與了問卷調查?
(2)算出表中a、b的值.
(注:計算中涉及到的“人數”均精確到1)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】【閱讀理解】
若![]() ,
, ![]() ,
, ![]() 為數軸上三點,若點
為數軸上三點,若點![]() 到
到![]() 的距離是點
的距離是點![]() 到
到![]() 的距離的
的距離的![]() 倍,我們就稱點
倍,我們就稱點![]() 是
是![]() 的優點.例如,如圖①,點
的優點.例如,如圖①,點![]() 表示的數為
表示的數為![]() ,點
,點![]() 表示的數為
表示的數為![]() .表示數
.表示數![]() 的點
的點![]() 到點
到點![]() 的距離是
的距離是![]() ,到點
,到點![]() 的距離是
的距離是![]() ,那么點
,那么點![]() 是
是![]() 的優點;又如,表示
的優點;又如,表示![]() 的點
的點![]() 到點
到點![]() 的距離是
的距離是![]() ,到點
,到點![]() 的距離是
的距離是![]() ,那么但點
,那么但點![]() 是
是![]() 的好點.
的好點.
【知識運用】
如圖②,![]() 、
、![]() 為數軸上兩點,點
為數軸上兩點,點![]() 所表示的數為
所表示的數為![]() ,點
,點![]() 所表示的數為
所表示的數為![]() .
.
(![]() )數__________所表示的點是
)數__________所表示的點是![]() 的優點.
的優點.
(![]() )如圖③,
)如圖③,![]() ,
, ![]() 為數軸上兩點,點
為數軸上兩點,點![]() 所表示的數為
所表示的數為![]() ,點
,點![]() 所表示的數為
所表示的數為![]() .現有一只電子螞蟻
.現有一只電子螞蟻![]() 從點
從點![]() 出發,以
出發,以![]() 個單位每秒的速度向左運動,到達點
個單位每秒的速度向左運動,到達點![]() 停止.當
停止.當![]() 為何值時,
為何值時, ![]() 、
、![]() 和
和![]() 中恰有一個點為其余兩點的好點?(請直接寫出答案)
中恰有一個點為其余兩點的好點?(請直接寫出答案)


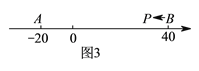
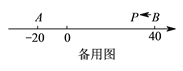
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com