
【題目】程大位所著《算法統宗》是一部中國傳統數學重要的著作.在《算法統宗》中記載:“平地秋千未起,踏板離地一尺.送行二步與人齊,五尺人高曾記.仕女佳人爭蹴,終朝笑語歡嬉.良工高士素好奇,算出索長有幾?”【注釋】1步=5尺.
譯文:“當秋千靜止時,秋千上的踏板離地有1尺高,如將秋千的踏板往前推動兩步(10尺)時,踏板就和人一樣高,已知這個人身高是5尺.美麗的姑娘和才子們,每天都來爭蕩秋千,歡聲笑語終日不斷.好奇的能工巧匠,能算出這秋千的繩索長是多少嗎?”
如圖,假設秋千的繩索長始終保持直線狀態,OA是秋千的靜止狀態,A是踏板,CD是地面,點B是推動兩步后踏板的位置,弧AB是踏板移動的軌跡.已知AC=1尺,CD=EB=10尺,人的身高BD=5尺.設繩索長OA=OB=x尺,則可列方程為 
科目:初中數學 來源: 題型:
【題目】已知:AB是⊙O的直徑,DA、DC分別是⊙O的切線,點A、C是切點,連接DO交弧AC于點E,連接AE、CE.
(1)如圖1,求證:EA=EC;
(2)如圖2,延長DO交⊙O于點F,連接CF、BE交于點G,求證:∠CGE=2∠F;
(3)如圖3,在(2)的條件下,DE=![]() AD,EF=2
AD,EF=2![]() , 求線段CG的長.
, 求線段CG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
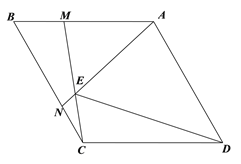
【題目】如圖菱形ABCD中,∠ADC=60°,M、N分別為線段AB,BC上兩點,且BM=CN,且AN,CM所在直線相交于E.
(1)證明△BCM≌△CAN;
(2)∠AEM= °;
(3)求證DE平分∠AEC;
(4)試猜想AE,CE,DE之間的數量關系并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,O是等邊△ABC內一點,連接OA、OB、OC,且OA=3,OB=4,OC=5,將△BAO繞點B順時針旋轉后得到△BCD,連接OD.求:
①旋轉角是____度;
②線段OD的長為_____;
③求∠BDC的度數.
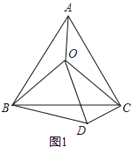
(2)如圖2所示,O是等腰直角△ABC(∠ABC=90°)內一點,連接OA、OB、OC,∠A0B=135,OA=1,0B=2,求0C的長.
小明同學借用了圖1的方法,將△BAO繞點B順時針旋轉后得到△BCD,請你繼續用小明的思路解答,或是選擇自己的方法求解.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,⊙C的半徑為r,點P是與圓心C不重合的點,給出如下定義:若點P′為射線CP上一點,滿足CPCP′=r2 , 則稱點P′為點P關于⊙C的反演點.右圖為點P及其關于⊙C的反演點P′的示意圖.
(1)如圖1,當⊙O的半徑為1時,分別求出點M(1,0),N(0,2),T(![]() ,
, ![]() )關于⊙O的反演點M′,N′,T′的坐標;
)關于⊙O的反演點M′,N′,T′的坐標;
(2)如圖2,已知點A(1,4),B(3,0),以AB為直徑的⊙G與y軸交于點C,D(點C位于點D下方),E為CD的中點.
①若點O,E關于⊙G的反演點分別為O′,E′,求∠E′O′G的大小;
②若點P在⊙G上,且∠BAP=∠OBC,設直線AP與x軸的交點為Q,點Q關于⊙G的反演點為Q′,請直接寫出線段GQ′的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在長和寬分別是a,b的長方形的四個角都剪去一個邊長為x的正方形,折疊后,做成一無蓋的盒子(單位:cm).
(1)用a,b,x表示紙片剩余部分的面積;
(2)用a,b,x表示盒子的體積;
(3)當a=10,b=8且剪去的每一個小正方形的面積等于4 cm2時,求剪去的每一個正方形的邊長及所做成的盒子的體積.

查看答案和解析>>
科目:初中數學 來源: 題型:
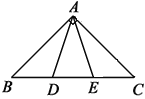
【題目】如圖,在△ABC中, ∠BAC=90°, AB=AC=2![]() ,點D,E均在邊BC上,且∠DAE=45°,若BD=1,則DE=__________.
,點D,E均在邊BC上,且∠DAE=45°,若BD=1,則DE=__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知A(n,﹣2),B(1,4)是一次函數y=kx+b的圖象和反比例函數y=![]() 的圖象的兩個交點,直線AB與y軸交于點C.
的圖象的兩個交點,直線AB與y軸交于點C.
(1)求反比例函數和一次函數的關系式;
(2)求△AOC的面積;
(3)求不等式kx+b﹣![]() <0的解集.(直接寫出答案)
<0的解集.(直接寫出答案)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com