【題目】如圖，點A．B在反比例函數y=
的圖象上，且點A，B的橫坐標分別為a，2a（a＜0），若S△AOB=3，則k的值為（ ）
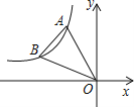
A.5B.-5C.4D.-4
【答案】B
【解析】
過A作AC⊥y軸于點C，過點B作BD⊥x軸于點D，延長DB和CA交于點E，由點A．B的橫坐標結合反比例函數圖象上點的坐標特征即可求出A．B點的坐標，進而得出點E的坐標，再利用分割圖形法求△AOB的面積結合S△AOB=3，即可得出關于k的一元一次方程，解方程即可得出結論．
過A作AC⊥y軸于點C，過點B作BD⊥x軸于點D，延長DB和CA交于點E，如圖所示．
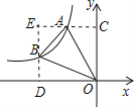
∵點A、B在反比例函數y=
的圖象上，且點A，B的橫坐標分別為a，2a（a＜0），
∴A(a，
)，B(2a，
)，E(2a，)，
∴OD=-2a，OC=，BE=，AE=-a，其中k+1＜0．
∴S△AOB=S矩形OCED-S△OBD-S△OAC-S△ABE=ODOC-
|k+1|-|k+1|-AEBE=3，
∵k+1＜0，
∴-
(k+1)=3，
解得：k=-5．
故選：B．
浙大優學小學年級銜接捷徑浙江大學出版社系列答案科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠ACB=90°，CD是AB邊上的高，∠BAC的平分線AE交C于F，EG⊥AB于G，請判斷四邊形GECF的形狀，并證明你的結論．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，四邊形ABCD的各頂點坐標分別為A（1，0），B（2，0），C（2，2），D（0，1）；四邊形BFGH的各頂點坐標分別為F（4，0），G（4，4），H（0，2）．則下列說法正確的是（ ）
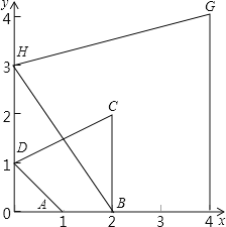
A.四邊形ABCD與四邊形BFGH相似但不位似
B.四邊形ABCD與四邊形BFGH位似但不相似
C.四邊形ABCD與四邊形BFGH位似，且位似比為l：
D.四邊形ABCD與四邊形BFGH位似，且位似比為l：2
查看答案和解析>>
科目：初中數學 來源： 題型：
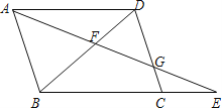
【題目】如圖，E為ABCD的邊BC延長線上一點，AE與BD交于點F，與DC交于點G．
（1）寫出所有與△ABE相似的三角形，并選擇其中一對相似三角形加以證明；
（2）若BC=2CE，求
的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
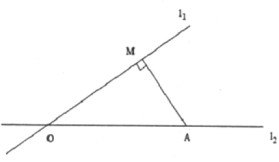
【題目】如圖，兩條公路
、
交予點
，在公路旁有一學校
，與點的距離為
，點（學校）到公路的距離
為
．一大貨車從點出發，行駛在公路上，汽車周圍
范圍內有噪音影響．
（1）貨車開過學校是否受噪音影響？為什么？
（2）若汽車速度為
，則學校受噪音影響多少秒鐘？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，∠BAC的平分線與BC的垂直平分線相交于點D，DE⊥AB，DF⊥AC，垂足分別為E、F，AB＝6，AC＝3，則BE長度為（ ）
A.1B.1.5C.2D.2.5
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某車庫出口處設置有“兩段式欄桿”，點A是欄桿轉動的支點，點E是欄桿兩段的連接點，當車輛經過時，欄桿AEF升起后的位置如圖1所示（圖2為其幾何圖形）．其中AB⊥BC，DC⊥BC，EF∥BC，∠EAB=150°，AB=AE=1.2m，BC=2.4m．
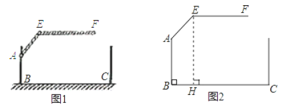
（1）求圖2中點E到地面的高度（即EH的長．
≈1.73，結果精確到0.01m，欄桿寬度忽略不計）；
（2）若一輛廂式貨車的寬度和高度均為2m，這輛車能否駛入該車庫？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某超市準備購進甲、乙兩種品牌的文具盒，甲、乙兩種玩具盒的進價和售價如下表，預計購進乙品牌文具盒的數量y（個）與甲品牌玩具盒數量x（個）之間的函數關系如圖所示．
甲 | 乙 | |
進價（元） | 15 | 30 |
售價（元） | 20 | 38 |
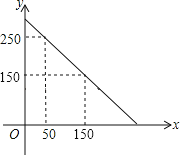
（1）y與x之間的函數關系式是 ；
（2）若超市準備用不超過6000元購進甲、乙兩種文具盒，則至少購進多少個甲種文具盒？
（3）在（2）的條件下，寫出銷售所得的利潤W（元）與x（個）之間的關系式，并求出獲得的最大利潤．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
