【題目】為慶祝“六一”兒童節，某市中小學統一組織文藝匯演，甲、乙兩所學校共92人(其中甲校人數多于乙校人數，且甲校人數不夠90人)準備統一購買服裝參加演出，下面是某服裝廠給出的演出服裝的價格表：
購買服裝的套數 | 1套至45套 | 46套至90套 | 91套及以上 |
每套服裝的價格 | 60元 | 50元 | 40元 |
如果兩校分別單獨購買服裝，一共應付5000元．
(1)如果甲、乙兩校聯合起來購買服裝，那么比各自購買服裝共可以節省多少錢？
(2)甲、乙兩校各有多少學生準備參加演出？
(3)如果甲校有10名同學抽調去參加書法繪畫比賽不能參加演出，請為兩校設計一種省錢的購買服裝方案．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
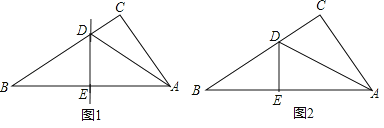
【題目】小王剪了兩張直角三角形紙片，進行了如下的操作：
（1）如圖1，將Rt△ABC沿某條直線折疊，使斜邊的兩個端點A與B重合，折痕為DE，若AC=6cm，BC=8cm，求CD的長.
（2）如圖2，小王拿出另一張Rt△ABC紙片，將直角邊AC沿直線AD折疊，使它落在斜邊AB上，且與AE重合，若AC=6cm，BC=8cm，求CD的長
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀材料：
我們知道|x|=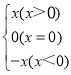
，現在我們可以用這一結論來化簡含有絕對值的代數式，如化簡代數式|x+1|+|x-2|時，可令x+1=0和x-2=0，分別求得x=-1，x=2（稱-1，2分別為|x+1|與|x-2|的零點值），在實數范圍內，零點值x=-1和x=2可將全體實數分成不重復且不遺漏的如下3種情況：
（1）當x＜-1時，原式=-（x+1）-（x-2）=-2x+1；
（2）當-1≤x＜2時，原式=x+1-（x-2）=3；
（3）當x≥2時，原式=x+1+x-2=2x-1．綜上所述，原式=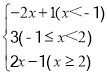
學以致用：
（Ⅰ）分別求出|x+3|和|x-1|的零點值；
（Ⅱ）化簡代數式|x+3|+|x-1|；
拓展應用：
（Ⅲ）求函數y=|x+3|+|x-1|（-3≤x≤3）的最大值和最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列條件中，不能判定四邊形是平行四邊形的是（ ）
A. 對角線互相平分B. 兩組對邊分別相等
C. 對角線互相垂直D. 一組對邊平行，一組對角相等
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，二次函數
（a＞0）圖象的頂點為D，其圖象與x軸的交點A、B的橫坐標分別為﹣1和3，則下列結論正確的是（ ）
A. 2a﹣b=0
B. a+b+c＞0
C. 3a﹣c=0
D. 當a=
時，△ABD是等腰直角三角形
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
