
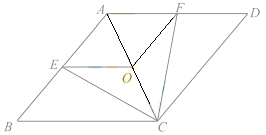
【題目】已知:如圖,在菱形ABCD 中,點E,O,F 分別是邊AB,AC,AD的中點,連接CE、CF、OF.
(1)求證:△ BCE≌△DCF;
(2)當AB與BC滿足什么條件時,四邊形AEOF正方形?請說明理由.
【答案】(1)證明見解析(2)四邊形AEOF是正方形
【解析】
試題分析:(1)利用SAS證明△ BCE≌△DCF;
(2)先證明AEOF為菱形,當BC⊥AB,得∠BAD=90°,再利用知識點:有一個角是90°的菱形是正方形。
試題解析:(1)∵四邊形ABCD為菱形
∴AB=BC=CD=DA,∠B=∠D
又E、F分別是AB、AD中點,∴BE=DF
∴△ABE≌△CDF(SAS)
(2)若AB⊥AD,則AEOF為正方形,理由如下
∵E、O分別是AB、AC中點,∴EO∥BC,
又BC∥AD,∴OE∥AD,即:OE∥AF
同理可證OF∥AE,所以四邊形AEOF為平行四邊形
由(1)可得AE=AF
所以平行四邊AEOF為菱形
因為BC⊥AB,所以∠BAD=90°,所以菱形AEOF為正方形。


 文敬圖書課時先鋒系列答案
文敬圖書課時先鋒系列答案科目:初中數學 來源: 題型:
【題目】某校為了豐富學生的校園生活,準備購進一批籃球和足球.其中籃球的單價比足球的單價多40元,用1500元購進的籃球個數與900元購進的足球個數相等.
(1)籃球和足球的單價各是多少元?
(2)該校打算用1000元購買籃球和足球,問恰好用完1000元,并且籃球、足球都買有的購買方案有哪幾種?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線PA經過點A(-1,0)、點P(1,2),直線PB是一次函數y=-x+3的圖象.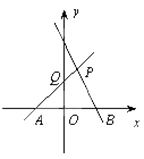
(1)求直線PA的表達式及Q點的坐標;
(2)求四邊形PQOB的面積;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com