
【題目】小明、小強從同一地點A同時反向(小明按逆時針方向,小強按順時針方向)繞環形跑道跑步,小明的速度為4a 米/秒,小強的速度為5a 米/秒(a>0),經過t秒兩人第一次相遇.
⑴ 這條環形跑道的周長為多少米?
⑵ 兩人第一次相遇后,小明、小強繼續按原方向繞跑道跑步. ① 小明又經過幾秒再次到達A點?
② 在①中當小明到達A點時,小強是否已經過A點?如果已經過,則小強經過A點后又走了多少米?如果沒有經過,請說明理由.
 全優點練單元計劃系列答案
全優點練單元計劃系列答案科目:初中數學 來源: 題型:
【題目】在四邊形ABCD中,AB=CD,M、N分別是AD和BC的中點,延長BA和CD分別交射線NM于點E和點F,若tan∠F=![]() , FC=FN,EN=
, FC=FN,EN=![]() , 則EF=
, 則EF= 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知頂點為(﹣3,﹣6)的拋物線y=ax2+bx+c經過點A,點(﹣2,m)和(﹣5,n)在該拋物線上,則下列結論中不正確的是( )
A.![]() >4ac
>4ac
B.m>n
C.方程a![]() +bx+c=﹣4的兩根為﹣5或﹣1
+bx+c=﹣4的兩根為﹣5或﹣1
D.a![]() +bx+c≥﹣6
+bx+c≥﹣6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖某超市舉行“翻牌”抽獎活動,在一張木板上共有6個相同的牌,其分別對應價值為2元、5元、8元、10元、20元和50元的獎品.
(1)小雷在該抽獎活動中隨機翻一張牌,求抽中10元獎品的概率;
(2)如果隨機翻兩張牌,且第一次翻過的牌不再參加下次翻牌,求兩次抽中的獎品的總價值大于14元的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明是個愛探究的學生,在學習完等腰三角形的判定定理之后,對于等腰![]() (如圖甲),若
(如圖甲),若![]() ,
,![]() ,小明發現,只要作
,小明發現,只要作![]() 的平分線就可以將
的平分線就可以將![]() 分成兩個等腰三角形.
分成兩個等腰三角形.
(1)你認為小明的發現正確嗎?若正確,請給出證明過程;若不正確,請說明理由;
(2)請你對圖乙的三角形進行探索,將![]() 分成兩個等腰三角形,并寫出頂角度數;
分成兩個等腰三角形,并寫出頂角度數;
(3)請你對圖丙的三角形進行再探索,將![]() 分成三個等腰三角形,并寫出頂角度數.
分成三個等腰三角形,并寫出頂角度數.



查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】老師在課堂上出了一個問題:若點A(﹣2,y1),B(1,y2)和C(4,y3)都在反比例函數y=![]() 的圖象上,比較y1 , y2 , y3的大小.
的圖象上,比較y1 , y2 , y3的大小.
小明是這樣思考的:當k<0時,反比例函數的圖象是y隨x的增大而增大的,并且﹣2<1<4,所以y1<y2<y3 .
你認為小明的思考 (填“正確”和“不正確”),理由是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】北京聯合張家口成功申辦2022年冬奧會后,滑雪運動已成為人們喜愛的娛樂健身項目.如圖是某滑雪場為初學者練習用的斜坡示意圖,出于安全因素考慮,決定將斜坡的傾角由45°降為30°,已知原斜坡坡面AB長為200米,點D,B,C在同一水平地面上,求改善后的斜坡坡角向前推進的距離BD.(結果保留整數.參考數據:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】奧林匹克公園觀光塔由五座高度不等、錯落有致的獨立塔組成.在綜合實踐活動課中,某小組的同學決定利用測角儀測量這五座塔中最高塔的高度(測角儀高度忽略不計).他們的操作方法如下:如圖,他們先在B處測得最高塔塔頂A的仰角為45°,然后向最高塔的塔基直行90米到達C處,再次測得最高塔塔頂A的仰角為58°.請幫助他們計算出最高塔的高度AD約為多少米.(參考數據:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)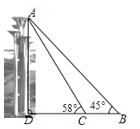
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com