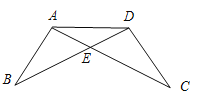
【題目】在一次數學課上，王老師在黑板上畫出一幅圖，并寫下了四個等式：
①
，②
，③
，④
．
（1）上述四個條件中，由哪兩個條件可以判定
是等腰三角形？用序號寫出所有成立的情形．
（2）請選擇(1)中的一種情形，寫出證明過程．
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】閱讀下列材料：一般地，
個相同的因數
相乘 
，記為
．如
，此時，
叫做以
為底
的對數，記為
（即
）．一般地，若
，（
且
，
），則叫做以為底
的對數，記為
（即
）．如
，則
叫做以為底
的對數，記為
（即
）．
（1）計算以下各對數的值：
__________，
__________，
__________．
（2）觀察（1）中三數、
，
之間滿足怎樣的關系式，
、
、
之間又滿足怎樣的關系式；
（3）由（2）的結果，你能歸納出一個一般性的結論嗎？
__________．（且，
，
）
（4）根據冪的運算法則：
以及對數的含義證明上述結論．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】蘇州太湖養殖場計劃養殖蟹和貝類產品，這兩個品種的種苗的總投放量只有50噸，根據經驗測算，這兩個品種的種苗每投放一噸的先期投資，養殖期間的投資以及產值如下表（單位：萬元/噸）
品種 | 先期投資 | 養殖期間投資 | 產值 |
貝類產品 | 0.9 | 0.3 | 0.33 |
蟹產品 | 0.4 | 1 | 2 |
養殖場受經濟條件的影響，先期投資不超過36萬元，養殖期間的投資不超過29萬元，設貝類的種苗投放量為x噸，
（1）求x的取值范圍；
（2）設這兩個品種產出后的總產值為y（萬元），試寫出y與x之間的函數關系式，并求出當x等于多少時，y有最大值？最大值是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
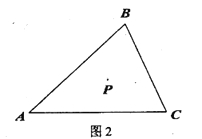
【題目】P是三角形
內一點，射線PD//AC ，射線PB//AB .
（1）當點D,E分別在AB,BC 上時，
①補全圖1：
②猜想
與
的數量關系，并證明；，
（2）當點
都在線段
上時，請先畫出圖形，想一想你在（1）中所得結論是否仍然成立？若成立，請證明；若不成立，請說明理由
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列說法中正確的是 ( )
A. 在 Rt△ABC中，若tanA＝
，則a＝4，b＝3
B. 在 Rt△ABC中，∠C＝90°，則tanA＋tanB＝1
C. 在 Rt△ABC 中，∠C＝90°，若a＝3，b＝4，則tanA＝
D. tan75°＝tan(45°＋30°)＝tan45°＋tan30°＝1＋
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線AB與坐標軸分別交于A（﹣2，0），B（0，1）兩點，與反比例函數的圖象在第一象限交于點C（4，n），求一次函數和反比例函數的解析式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，某辦公樓AB的后面有一建筑物CD，當光線與地面的夾角是22°時，辦公樓在建筑物的墻上留下高3米的影子CE，而當光線與地面夾角是45°時，辦公樓頂A在地面上的影子F與墻角C有27米的距離（B，F，C在一條直線上）．
（1）求辦公樓AB的高度；
（2）若要在A，E之間掛一些彩旗，請你求出A，E之間的距離．
（參考數據：sin22°≈
，cos22°≈
，tan22°≈
）
查看答案和解析>>
科目：初中數學 來源： 題型：
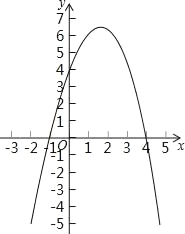
【題目】已知二次函數y=﹣x2+3x+4的圖象如圖：（直接寫答案）
（1）方程﹣x2+3x+4=0的解是 ；
（2）不等式﹣x2+3x+4＞0的解集是 ；
（3）不等式﹣x2+3x+4＜0的解集是 ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
