【題目】如圖，在平面直角坐標系中，拋物線y=x2經過平移得到拋物線y=x2﹣2x ， 其對稱軸與兩拋物線所圍成的陰影部分的面積是 ．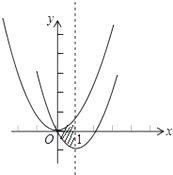 
【答案】1
【解析】先利用配方法得到拋物線y=x2-2x的頂點坐標為（1，-1），則拋物線y=x2向右平移1個單位，向下平移1個單位得到拋物線y=x2-2x，然后利用陰影部分的面積等于三角形面積進行計算． 解：y=x2-2x=（x-1）2-1，即平移后拋物線的頂點坐標為（1，-1）， 所以拋物線y=x2向右平移1個單位，向下平移1個單位得到拋物線y=x2-2x， 所以對稱軸與兩拋物線所圍成的陰影部分的面積= 
×1×2=1． 故答案為1．
根據已知可知兩圖像是通過平移得到的，因此它們的形狀和大小一樣，先求出平移后的頂點坐標，及對稱軸，要求其對稱軸與兩拋物線所圍成的陰影部分的面積轉化為求三角形的面積，即可求出結果。
期末沖刺100分創新金卷完全試卷系列答案科目：初中數學 來源： 題型：
【題目】如圖，等腰Rt△ABC（∠ACB=90°）的直角邊與正方形DEFG的邊長均為2，且AC與DE在同一直線上，開始時點C與點D重合，讓△ABC沿這條直線向右平移，直到點A與點E重合為止．設CD的長為x，△ABC與正方形DEFG重合部分（圖中陰影部分）的面積為y，則y與x之間的函數關系的圖象大致是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】計算：
(1)a(a－3)－(－a＋
)(－a－)；
(2)(2x－y)(y＋2x)－4(y－x)(－x－y)；
(3)(3a＋1)(9a2＋1)(3a－1)；
(4)(1－x)(1＋x2)(1＋x)(1＋x4)．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，已知點A(a－1，a＋b)，B(a，0)，且|a＋b－3|＋(a－2b)2＝0，C為x軸上點B右側的動點，以AC為腰作等腰三角形ACD，使AD＝AC，∠CAD＝∠OAB，直線DB交y軸于點P.
(1)求證：AO＝AB；
(2)求證：△AOC≌△ABD；
(3)當點C運動時，點P在y軸上的位置是否發生改變，為什么？
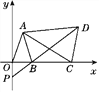
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，ABCD的對角線AC，BD交于點O，AE平分∠BAD交BC于點E，且∠ADC＝60°，AB＝
BC，連結OE.下列結論：
①∠CAD＝30°；②SABCD＝AB·AC；③OB＝AB；④OE＝
BC，成立的結論有______．(填序號)
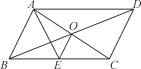
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小明在他家里的時鐘上安裝了一個電腦軟件，他設定當鐘聲在n點鐘響起后，下一次則在（3n﹣1）小時后響起，例如鐘聲第一次在3點鐘響起，那么第2次在（3×3﹣1=8）小時后，也就是11點響起，第3次在（3×11﹣1=32）小時后，即7點響起，以此類推…；現在第1次鐘聲響起時為2點鐘，那么第3次響起時為點，第2017次響起時為點（如圖鐘表，時間為12小時制）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，BD是△ABC的角平分線，它的垂直平分線分別交AB、BC于點E、F、G，連接ED、DG．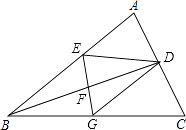 
（1）請判斷四邊形EBGD的形狀，并說明理由；
（2）若∠ABC=30°，∠C=45°，ED=2，求GC的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在長方形
中，邊
，
，以點
為原點，
，
所在的直線為
軸和
軸，建立直角坐標系.
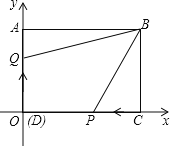
（1）點
的坐標為
，則
點坐標為______，
點坐標為______；
（2）當點
從出發，以2單位/秒的速度沿
方向移動（不過點），
從原點出發以1單位/秒的速度沿方向移動（不過點），，同時出發，在移動過程中，四邊形
的面積是否變化？若不變，求其值；若變化，求其變化范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
