
【題目】閱讀材料:對任意一個三位數![]() 如果
如果![]() 滿足各個數位上的數字互不相同,且都不為零,那么稱這個數為“相異數”,將一個“相異數”任意兩個數位上的數字對調后可以得到三個不同的新三位數,把這三個新三位數的和與
滿足各個數位上的數字互不相同,且都不為零,那么稱這個數為“相異數”,將一個“相異數”任意兩個數位上的數字對調后可以得到三個不同的新三位數,把這三個新三位數的和與![]() 的商記為
的商記為![]() .例如
.例如![]() 對調百位與十位上的數字得到
對調百位與十位上的數字得到![]() 對調百位與個位上的數字得到
對調百位與個位上的數字得到![]() 對調十位與個位上的數字得到
對調十位與個位上的數字得到![]() 這三個新三位數的和為
這三個新三位數的和為![]() 所以
所以![]() .試根據以上信息,完成下列問題:
.試根據以上信息,完成下列問題:
(1)計算:![]() __,
__,![]() __,你從中發現什么規律?你發現規律是:__.
__,你從中發現什么規律?你發現規律是:__.
(2)若![]() 都是“相異數”,
都是“相異數”,![]()
![]() ,其中x是正整數),是否存在
,其中x是正整數),是否存在![]() 滿足
滿足![]() ,若存在,請求出這個
,若存在,請求出這個![]() ,若不存在,請說明理由.
,若不存在,請說明理由.
【答案】(1)9,13,規律為:![]() 一定是個正整數,且
一定是個正整數,且![]() 等于原三位數各個數位上的數字之和;(2)不存在,理由見解析
等于原三位數各個數位上的數字之和;(2)不存在,理由見解析
【解析】
(1)根據“相異數”的定義可求,進而可得規律;
(2)根據(1)可知F(s)=x+5,F(t)=6+x,根據![]() 列出方程求得x的值,進而可得結果.
列出方程求得x的值,進而可得結果.
解:(1)F(243)=(423+342+234)÷111=9,
F(517)=(157+571+715)÷111=13,
故答案為:9,13,規律為:![]() 一定是個正整數,且
一定是個正整數,且![]() 等于原三位數各個數位上的數字之和;
等于原三位數各個數位上的數字之和;
(2)∵s,t都是“相異數”,s=100x+32,t=150+x,
∴由(1)得F(s)=x+3+2=x+5,F(t)=1+5+x=6+x,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得![]() ,
,
∵![]() 不是正整數,
不是正整數,
∴不存在符合題意的x使得![]() ,
,
故答案為不存在符合題意的x.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案科目:初中數學 來源: 題型:
【題目】把一副撲克牌中的三張黑桃牌(它們的正面數字分別為3、4、5)洗勻后正面朝下放在桌面上.小王和小李玩摸牌游戲,游戲規則如下:先由小王隨機抽取一張牌,記下牌面數字后放回,洗勻后正面朝下,再由小李隨機抽取一張牌,記下牌面數字.當兩張牌的牌面數字相同時,小王贏;當兩張牌的牌面數字不同時,小李贏.現請你分析游戲規則對雙方是否公平,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示是鼎龍高速路口開往寧都方向的某汽車行駛的路程s(km)與時間t(分鐘)的函數關系圖,觀察圖中所提供的信息,解答下列問題: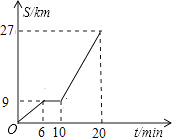
(1)汽車在前6分鐘內的平均速度是千米/小時,汽車在興國服務區停了多長時間?分鐘;
(2)當10≤t≤20時,求S與t的函數關系式;
(3)規定:高速公路時速超過120千米/小時為超速行駛,試判斷當10≤t≤20時,該汽車是否超速,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線AB∥CD.
(1)如圖1,請直接寫出∠BME、∠E、∠END的數量關系為 ;
(2)如圖2,∠BME與∠CNE的角平分線所在的直線相交于點P,試探究∠P與∠E之間的數量關系,并證明你的結論;
(3)如圖3,∠ABM=![]() ∠MBE,∠CDN=
∠MBE,∠CDN=![]() ∠NDE,直線MB、ND交于點F,則
∠NDE,直線MB、ND交于點F,則![]() =___.
=___.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合題
(1)如圖1,銳角△ABC中,AD⊥BC于D,BE⊥AC于E,AD與BE交于F,連DE,求證:DFDA=DBDC;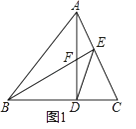
(2)如圖2,若∠BAC=90°,AD⊥BC于D,F為線段AD上一點,在AD延長線上找一點G使AD2=DFDG,請畫出圖形找出點G并加以證明;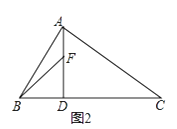
(3)如圖3,在(1)的條件下,若∠ABC=45°,EF=1,EC=3,直接寫出BD長.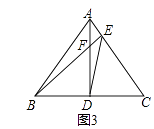
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將△ABC向右平移3個單位長度,再向上平移2個單位長度,可以得到![]() .
.

(1)畫出平移后的![]() ;
;
(2)寫出![]() 三個頂點的坐標;
三個頂點的坐標;
(3)已知點P在x軸上,以![]() 、
、![]() 、P為頂點的三角形面積為4,求點P的坐標.
、P為頂點的三角形面積為4,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】玲玲和牛牛相約在小區筆直的步行道上健步走鍛煉身體.兩人都從步行道起點![]() 向終點
向終點![]() 走去.牛牛出發
走去.牛牛出發![]() 分鐘后,玲玲出發.又過了
分鐘后,玲玲出發.又過了![]() 分鐘,牛牛停下來接了
分鐘,牛牛停下來接了![]() 分鐘的電話,玲玲則以原速繼續步行,與牛牛相遇后,玲玲的速度減少到原來的
分鐘的電話,玲玲則以原速繼續步行,與牛牛相遇后,玲玲的速度減少到原來的![]() 走向終點
走向終點![]() .牛牛接完電話后,提高速度向終點
.牛牛接完電話后,提高速度向終點![]() 走去,
走去,![]() 分鐘后剛好追上玲玲,到達終點
分鐘后剛好追上玲玲,到達終點![]() 后立即調頭以提速后的速度返回起點
后立即調頭以提速后的速度返回起點![]() (調頭時間忽略不計),玲玲、牛牛兩人相距的路程
(調頭時間忽略不計),玲玲、牛牛兩人相距的路程![]() (米)與牛牛出發的時間
(米)與牛牛出發的時間![]() (分鐘)之間的關系如圖所示.
(分鐘)之間的關系如圖所示.

(1)牛牛開始健步走的速度為_______米/分;
(2)求玲玲開始健步走的速度和牛牛提速后的速度;
(3)玲玲走到終點![]() 后,停下來休息了一會兒.牛牛回到起點
后,停下來休息了一會兒.牛牛回到起點![]() 后,立即調頭仍以提速后的速度走向終點
后,立即調頭仍以提速后的速度走向終點![]() ,玲玲休息
,玲玲休息![]() 分鐘后以減速后的速度調頭走向起點
分鐘后以減速后的速度調頭走向起點![]() 兩人恰好在
兩人恰好在![]() 中點處相遇,求步行道
中點處相遇,求步行道![]() 的長度.
的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
(1)若∠BAC=50°,求∠EDA的度數;
(2)求證:直線AD是線段CE的垂直平分線.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com