
【題目】如圖,以直角三角形a、b、c為邊,向外作等邊三角形,半圓,等腰直角三角形和正方形,上述四種情況的面積關系滿足S1+S2=S3圖形個數有( ) 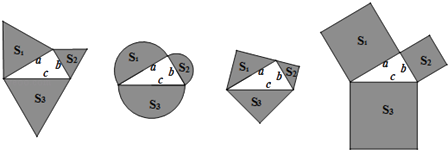
A.1
B.2
C.3
D.4
【答案】D
【解析】解:(1)S1= ![]() a2 , S2=
a2 , S2= ![]() b2 , S3=
b2 , S3= ![]() c2 , ∵a2+b2=c2 ,
c2 , ∵a2+b2=c2 ,
∴ ![]() a2+
a2+ ![]() b2=
b2= ![]() c2 ,
c2 ,
∴S1+S2=S3 .
·(2)S1= ![]() a2 , S2=
a2 , S2= ![]() b2 , S3=
b2 , S3= ![]() c2 ,
c2 ,
∵a2+b2=c2 ,
∴ ![]() a2+
a2+ ![]() b2=
b2= ![]() c2 ,
c2 ,
∴S1+S2=S3 .
·(3)S1= ![]() a2 , S2=
a2 , S2= ![]() b2 , S3=
b2 , S3= ![]() c2 ,
c2 ,
∵a2+b2=c2 ,
∴ ![]() a2+
a2+ ![]() b2=
b2= ![]() c2 ,
c2 ,
∴S1+S2=S3 .
·(4)S1=a2 , S2=b2 , S3=c2 ,
∵a2+b2=c2 ,
∴S1+S2=S3 .
綜上,可得
面積關系滿足S1+S2=S3圖形有4個.
故選:D.
根據直角三角形a、b、c為邊,應用勾股定理,可得a2+b2=c2 . ()第一個圖形中,首先根據等邊三角形的面積的求法,表示出3個三角形的面積;然后根據a2+b2=c2 , 可得S1+S2=S3 . (2)第二個圖形中,首先根據圓的面積的求法,表示出3個半圓的面積;然后根據a2+b2=c2 , 可得S1+S2=S3 . (3)第三個圖形中,首先根據等腰直角三角形的面積的求法,表示出3個等腰直角三角形的面積;然后根據a2+b2=c2 , 可得S1+S2=S3 . (4)第四個圖形中,首先根據正方形的面積的求法,表示出3個正方形的面積;然后根據a2+b2=c2 , 可得S1+S2=S3 .


科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD的對角線AC與BD相交于點O,CE∥BD,DE∥AC,AD=2 ![]() ,DE=2,則四邊形OCED的面積( )
,DE=2,則四邊形OCED的面積( ) 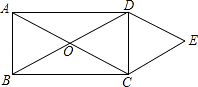
A.2 ![]()
B.4
C.4 ![]()
D.8
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com