【題目】計算：
（1）（﹣3）+40+（﹣32）+（﹣8）
（2）12﹣（﹣18）+（﹣7）
（3）（+3
）﹣（﹣5
）+（﹣2
）﹣（﹣32
）
（4）81.26﹣293.8+8.74+111
【答案】（1）-3；（2）23；（3）39
；（4）－92.8
【解析】
（1）根據互為相反數之和為0計算；
（2）先求出正數之和，根據根據異號兩數相加的法則計算；
（3）根據加法交換律把同分母的兩個數放在一起，計算即可；
（4）根據有理數的加減混合運算法則計算．
解：（1）（﹣3）+40+[（﹣32）+（﹣8）]
＝﹣3+（40﹣40）
＝﹣3；
（2）12﹣（﹣18）+（﹣7）
＝12+18﹣7
＝30﹣7
＝23；
（3）（+3
）﹣（﹣5
）+（﹣2
）﹣（﹣32
）
＝（+3﹣2）+（5+32）
＝1+38
＝39；
（4）81.26﹣293.8+8.74+111
＝81.26+8.74+111﹣293.8
＝90+111﹣293.8
＝201﹣293.8
＝﹣92.8．
科目：初中數學 來源： 題型：
【題目】如圖，在等邊三角形ABC中，AB=12cm，動點P從點A出發以1cm/s的速度沿AC勻速運動，動點Q同時從點B出發以同樣的速度沿CB的延長線方向勻速運動，當點P到達點C時，點P，Q同時停止運動.設運動時間為ts，過點P作PE⊥AB于點E，連接PQ交AB于點D.
⑴當t為何值時，△CPQ為直角三角形？
⑵求DE的長.
⑶取線段BC的中點M，連接PM，將△CPM沿直線PM翻折，得到△C，PM，連接AC，，當t= 時，AC，的值最小，最小值為 .
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在我市“青山綠水”行動中，某社區計劃對面積為
的區域進行綠化，經投標由甲、乙兩個工程隊來完成．已知甲隊每天能完成綠化的面積是乙隊每天能完成綠化面積的2倍，如果兩隊各自獨立完成面積為
區域的綠化時，甲隊比乙隊少用6天．
(1)求甲、乙兩工程隊每天各能完成多少面積的綠化；
(2)若甲隊每天綠化費用是1.2萬元，乙隊每天綠化費用為0.5萬元，社區要使這次綠化的總費用不超過40萬元，則至少應安排乙工程隊綠化多少天？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，小螞蟻在9×9的小方格上沿著網格線運動（每小格邊長為1），一只螞蟻在C處找到食物后，要通知A、B、D、E處的其他小螞蟻，我們把它的行動規定：向上或向右為正，向下或向左為負。如果從C到D記為：C→D（＋2，－3）（第一個數表示左、右方向，第二個數表示上、下方向），那么；
（1）C→B（ ），C→E（ ），D→ （－4，－3），D→ （ ，＋3）；
（2）若這只小螞蟻的行走路線為C→E→D→B→A→C，請你計算小螞蟻走過的路程．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，現有甲、乙兩個小分隊分別同時從B、C兩地出發前往A地，甲沿線路BA行進，乙沿線路CA行進，已知C在A的南偏東55°方向，AB的坡度為1：5，同時由于地震原因造成BC路段泥石堵塞，在BC路段中位于A的正南方向上有一清障處H，負責搶修BC路段，已知BH為12000m．
（1）求BC的長度；
（2）如果兩個分隊在前往A地時勻速前行，且甲的速度是乙的速度的三倍．試判斷哪個分隊先到達A地．（tan55°≈1.4，sin55°≈0.84，cos55°≈0.6，
≈5.01，結果保留整數）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】超速行駛是引發交通事故的主要原因之一．上周末，小明和三位同學嘗試用自己所學的知識檢測車速．如圖，觀測點設在A處，離益陽大道的距離(AC)為30米．這時，一輛小轎車由西向東勻速行駛，測得此車從B處行駛到C處所用的時間為8秒，∠BAC＝75°.
(1)求B、C兩點的距離；
(2)請判斷此車是否超過了益陽大道60千米/小時的限制速度？
(計算時距離精確到1米，參考數據：sin75°≈0.9659，cos75°≈0.2588，tan75°≈3.732， 
≈1.732，60千米/小時≈16.7米/秒)
查看答案和解析>>
科目：初中數學 來源： 題型：
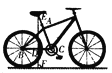
【題目】如圖所示的是一輛自行車的側面示意圖．已知車輪直徑為65 cm，車架中AC的長為42 cm，座桿AE的長為18 cm，點E，A，C在同一條直線上，后軸軸心B與中軸軸心C所在直線BC與地面平行，∠C＝73°，求車座E到地面的距離EF．(結果精確到l cm，參考數據：sin 73°≈0.96，cos 73°≈0.29，tan 73°≈3.27)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀材料：據說，我國著名數學家華羅庚在出國訪問途中，看到飛機上鄰座的乘客閱讀的雜志上有一道智力題：一個數是59319，希望求它的立方根.華羅庚脫口而出：39，鄰座的乘客十分驚奇，忙問計算的奧妙.
你知道華羅庚是怎樣迅速準確地計算出來的嗎？他是按照下面的方法確定的:
由
，
，就能確定
是2位數.由59319的個位上的數是9，就能確定的個位上的數是9，如果劃去59319后面的三位319得到數59，而
，
，由此可確定的十位上的數是3，所以，
.
（1）已知19683，110592都是整數的立方，按照上述方法，請直接寫出它們的立方根；
（2）
是我們沒有學習過的四次方根，且它的結果也是一個整數，請你根據材料的方法求出結果，并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
