
【題目】如圖,已知線段![]() ,點(diǎn)
,點(diǎn)![]() 為線段
為線段![]() 上的一個(gè)動(dòng)點(diǎn),點(diǎn)
上的一個(gè)動(dòng)點(diǎn),點(diǎn)![]() 分別是
分別是![]() 和
和![]() 的中點(diǎn).
的中點(diǎn).
(1)若點(diǎn)![]() 恰好是
恰好是![]() 中點(diǎn),則
中點(diǎn),則![]()
![]() ;
;
(2)若![]() ,求
,求![]() 的長;
的長;
(3)試?yán)?/span>“字母代替數(shù)”的方法,說明不論![]() 取何值(不超過
取何值(不超過![]() ),
),![]() 的長不變.
的長不變.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)見解析.
;(3)見解析.
【解析】
(1)點(diǎn)![]() 恰好是
恰好是![]() 中點(diǎn),AB=12,得出AC和CB的長度,根據(jù)點(diǎn)
中點(diǎn),AB=12,得出AC和CB的長度,根據(jù)點(diǎn)![]() 分別是
分別是![]() 和
和![]() 的中點(diǎn),得出DC和CE得長度,即可求解.
的中點(diǎn),得出DC和CE得長度,即可求解.
(2) AC=4cm,點(diǎn)D是AC的中點(diǎn),得出AD和DC的長度,根據(jù)AB=12cm,得出CB的長度,因點(diǎn)E是CB的中點(diǎn),得出CE的長度即可求解.
(3) )設(shè)AC=![]() cm,按照題(2)的思路即可得出DE=DC+CE=
cm,按照題(2)的思路即可得出DE=DC+CE=![]() +6-
+6-![]() =6cm,DE是一個(gè)定值,所以與AC無關(guān).
=6cm,DE是一個(gè)定值,所以與AC無關(guān).
解: (1)∵點(diǎn)![]() 恰好是
恰好是![]() 中點(diǎn),AB=12
中點(diǎn),AB=12
∴AC=CB=6cm
又∵點(diǎn)![]() 分別是
分別是![]() 和
和![]() 的中點(diǎn)
的中點(diǎn)
∴AD=DC=3cm,CE=EB=3cm
∴DE=DC+CE=3+3=6cm
(2)∵AC=4cm,點(diǎn)D是AC的中點(diǎn)
∴AD=CD=2cm
∵AB=12cm,點(diǎn)E是CB的中點(diǎn)
∴CB=2CE=2EB=12-4=8cm
∴CE=4cm
∴DE=DC+CE=4+2=6cm
(3)設(shè)AC=![]() cm
cm
∵點(diǎn)D是AC的中點(diǎn)
∴AD=CD=![]() cm
cm
∵AB=12cm,點(diǎn)E是CB的中點(diǎn)
∴CB=2CE=2EB=(12-![]() )cm
)cm
∴CE=(6-![]() )cm
)cm
∴DE=DC+CE=![]() +6-
+6-![]() =6cm
=6cm
∴DE的長度是一個(gè)定值,與AC無關(guān).


 99加1領(lǐng)先期末特訓(xùn)卷系列答案
99加1領(lǐng)先期末特訓(xùn)卷系列答案 百強(qiáng)名校期末沖刺100分系列答案
百強(qiáng)名校期末沖刺100分系列答案 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案 金狀元績優(yōu)好卷系列答案
金狀元績優(yōu)好卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
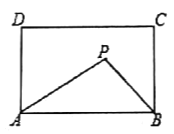
【題目】如圖所示,在矩形![]() 中,
中,![]() ,
,![]() ,矩形內(nèi)部有一動(dòng)點(diǎn)
,矩形內(nèi)部有一動(dòng)點(diǎn)![]() 滿足
滿足![]() ,則點(diǎn)
,則點(diǎn)![]() 到
到![]() ,
,![]() 兩點(diǎn)的距離之和
兩點(diǎn)的距離之和![]() 的最小值為( ).
的最小值為( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
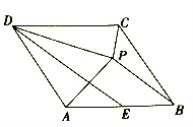
【題目】在菱形![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 邊的中點(diǎn),點(diǎn)
邊的中點(diǎn),點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 關(guān)于
關(guān)于![]() 對稱,連接
對稱,連接![]() 、
、![]() 、
、![]() ,下列結(jié)論:①
,下列結(jié)論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正確的是( )
,其中正確的是( )
A. ①②B. ①②③C. ①②④D. ①②③④
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】規(guī)律發(fā)現(xiàn):
在數(shù)軸上
(1)點(diǎn)M表示的數(shù)是2,點(diǎn)N表示的數(shù)是8,則線段MN的中點(diǎn)P表示的數(shù)為______;
(2)點(diǎn)M表示的數(shù)是﹣3,點(diǎn)N表示的數(shù)是7,則線段MN的中點(diǎn)P表示的數(shù)為_____;發(fā)現(xiàn):點(diǎn)M表示的數(shù)是a,點(diǎn)N表示的數(shù)是b,則線段MN的中點(diǎn)P表示的數(shù)為______.
直接運(yùn)用:
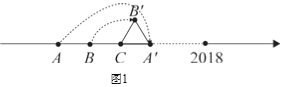
將數(shù)軸按如圖1所示,從點(diǎn)A開始折出一個(gè)等邊三角形A'B'C,設(shè)點(diǎn)A表示的數(shù)為x﹣3,點(diǎn)B表示的數(shù)為2x+1,C表示的數(shù)為x﹣1,則x值為_____,若將△A'B'C從圖中位置向右滾動(dòng),則數(shù)2018對應(yīng)的點(diǎn)將與△A'B'C的頂點(diǎn)_______重合.
類比遷移:
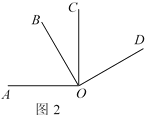
如圖2:OA⊥OC,OB⊥OD,∠COD=60°,若射線OA繞O點(diǎn)以每秒15°的速度順時(shí)針旋轉(zhuǎn),射線OB繞O點(diǎn)以每秒10°的速度順時(shí)針旋轉(zhuǎn),射線OC繞O點(diǎn)以每秒5°的速度逆時(shí)針旋轉(zhuǎn),三線同時(shí)旋轉(zhuǎn),當(dāng)一條射線與射線OD重合時(shí),三條射線同時(shí)停止運(yùn)動(dòng).
①求射線OC和射線OB相遇時(shí),∠AOB的度數(shù);
②運(yùn)動(dòng)幾秒時(shí),射線OA是∠BOC的平分線?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 在 數(shù)軸上對應(yīng)的數(shù)分別用
在 數(shù)軸上對應(yīng)的數(shù)分別用![]() 表示,且
表示,且![]() .
.![]() 是數(shù)軸的一動(dòng)點(diǎn).
是數(shù)軸的一動(dòng)點(diǎn).
⑴在數(shù)軸上標(biāo)出![]() 的位置,并求出
的位置,并求出![]() 之間的距離;
之間的距離;
⑵數(shù)軸上一點(diǎn)![]() 距
距![]() 點(diǎn)24個(gè)單位的長度,其對應(yīng)的數(shù)
點(diǎn)24個(gè)單位的長度,其對應(yīng)的數(shù)![]() 滿足
滿足![]() ,當(dāng)
,當(dāng)![]() 點(diǎn)滿足
點(diǎn)滿足![]() 時(shí),求
時(shí),求![]() 點(diǎn)對應(yīng)的數(shù).
點(diǎn)對應(yīng)的數(shù).
⑶動(dòng)點(diǎn)![]() 從原點(diǎn)開始第一次向左移動(dòng)1個(gè)單位,第二次向右移動(dòng)3個(gè)單位長度,第三次向左移動(dòng)5個(gè)單位長度,第四次向右移動(dòng)7個(gè)單位長度,……點(diǎn)
從原點(diǎn)開始第一次向左移動(dòng)1個(gè)單位,第二次向右移動(dòng)3個(gè)單位長度,第三次向左移動(dòng)5個(gè)單位長度,第四次向右移動(dòng)7個(gè)單位長度,……點(diǎn)![]() 能移動(dòng)到與
能移動(dòng)到與![]() 或
或![]() 重合的位置嗎?若能,請?zhí)骄康趲状我苿?dòng)時(shí)重合;若不能,請說明理由.
重合的位置嗎?若能,請?zhí)骄康趲状我苿?dòng)時(shí)重合;若不能,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
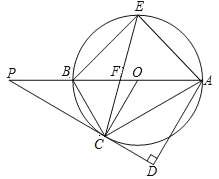
【題目】如圖所示,AB 是⊙O 的直徑,P 為 AB 延長線上的一點(diǎn),PC 切⊙O 于點(diǎn) C,AD⊥PC, 垂足為 D,弦 CE 平分∠ACB,交 AB 于點(diǎn) F,連接 AE.
(1)求證:PC=PF;
(2)若 tan∠ABC=![]() ,AE=5
,AE=5![]() ,求線段 PC 的長.
,求線段 PC 的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
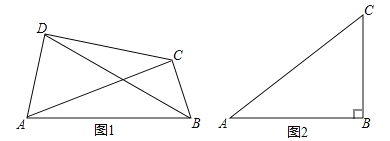
【題目】如圖1,在四邊形ABCD中,如果對角線AC和BD相交并且相等,那么我們把這樣的四邊形稱為等角線四邊形.
(1)①在“平行四邊形、矩形、菱形”中, 一定是等角線四邊形(填寫圖形名稱);
②若M、N、P、Q分別是等角線四邊形ABCD四邊AB、BC、CD.DA的中點(diǎn),當(dāng)對角線AC、BD還要滿足 時(shí),四邊形MNPQ是正方形.
(2)如圖2,已知△ABC中,∠ABC=90°,AB=4,BC=3,D為平面內(nèi)一點(diǎn).
①若四邊形ABCD是等角線四邊形,且AD=BD,則四邊形ABCD的面積是 ;
②設(shè)點(diǎn)E是以C為圓心,1為半徑的圓上的動(dòng)點(diǎn),若四邊形ABED是等角線四邊形,寫出四邊形ABED面積的最大值,并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩地相距300千米,一輛貨車和一輛轎車分別從甲地開往乙地(轎車的平均速度大于貨車的平均速度),如圖,線段![]() 、折線
、折線![]() 分別表示兩車離甲地的距離
分別表示兩車離甲地的距離![]() (單位:千米)與時(shí)間
(單位:千米)與時(shí)間![]() (單位:小時(shí))之間的函數(shù)關(guān)系.
(單位:小時(shí))之間的函數(shù)關(guān)系.
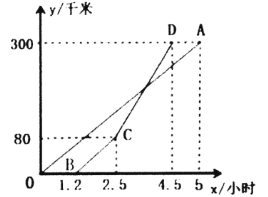
(1)線段![]() 與折線
與折線![]() 中,______(填線段
中,______(填線段![]() 或折線
或折線![]() )表示貨車離甲地的距離
)表示貨車離甲地的距離![]() 與時(shí)間
與時(shí)間![]() 之間的函數(shù)關(guān)系.
之間的函數(shù)關(guān)系.
(2)求線段![]() 的函數(shù)關(guān)系式(標(biāo)出自變量
的函數(shù)關(guān)系式(標(biāo)出自變量![]() 取值范圍);
取值范圍);
(3)貨車出發(fā)多長時(shí)間兩車相遇?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
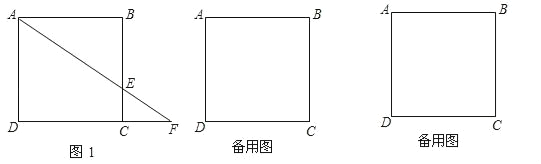
【題目】已知邊長為3的正方形ABCD中,點(diǎn)E在射線BC上,且BE=2CE,連接AE交射線DC于點(diǎn)F,若△ABE沿直線AE翻折,點(diǎn)B落在點(diǎn)B1處.
(1)如圖1,若點(diǎn)E在線段BC上,求CF的長;
(2)求sin∠DAB1的值;
(3)如果題設(shè)中“BE=2CE”改為“![]() =x”,其它條件都不變,試寫出△ABE翻折后與正方形ABCD公共部分的面積y與x的關(guān)系式及自變量x的取值范圍(只要寫出結(jié)論,不需寫出解題過程).
=x”,其它條件都不變,試寫出△ABE翻折后與正方形ABCD公共部分的面積y與x的關(guān)系式及自變量x的取值范圍(只要寫出結(jié)論,不需寫出解題過程).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com