
【題目】綜合與探究:
如圖1,拋物線![]() 與
與![]() 軸交于
軸交于![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側),頂點為
的左側),頂點為![]() ,
,![]() 為對稱軸右側拋物線的一個動點,直線
為對稱軸右側拋物線的一個動點,直線![]() 與
與![]() 軸于點
軸于點![]() ,過點
,過點![]() 作
作![]() ,交
,交![]() 軸于點
軸于點![]() .
.
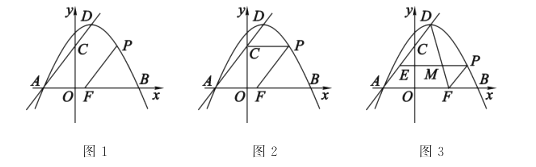
(1)求直線![]() 的函數(shù)表達式及點
的函數(shù)表達式及點![]() 的坐標;
的坐標;
(2)如圖2,當![]() 軸時,將
軸時,將![]() 以每秒1個單位長度的速度沿
以每秒1個單位長度的速度沿![]() 軸的正方向平移,當點
軸的正方向平移,當點![]() 與點
與點![]() 重合時停止平移.設平移
重合時停止平移.設平移![]() 秒時,在平移過程中
秒時,在平移過程中![]() 與四邊形
與四邊形![]() 重疊部分的面積為
重疊部分的面積為![]() ,求
,求![]() 關于
關于![]() 的函數(shù)關系式,并寫出自變量
的函數(shù)關系式,并寫出自變量![]() 的取值范圍;
的取值范圍;
(3)如圖3,過點![]() 作
作![]() 軸的平行線,交直線
軸的平行線,交直線![]() 于點
于點![]() ,直線
,直線![]() 與
與![]() 交于點
交于點![]() ,設點
,設點![]() 的橫坐標為
的橫坐標為![]() .
.
①當![]() 時,求
時,求![]() 的值;
的值;
②試探究點![]() 在運動過程中,是否存在值
在運動過程中,是否存在值![]() ,使四邊形
,使四邊形![]() 是菱形?若存在,請直接寫出點
是菱形?若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)![]() ,
,![]() ;(2)當
;(2)當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;(3)①
;(3)①![]() 或
或![]() ,②
,②![]()
【解析】
(1)先通過拋物線函數(shù)關系式求出與x軸的兩個交點A、B的坐標以及頂點D的坐標,再利用待定系數(shù)可求得直線AD的函數(shù)表達式,令x=0,即可求得點C的坐標;
(2)先求出點P坐標![]() ,通過平移可求得
,通過平移可求得![]() ,從而可得OF的長為
,從而可得OF的長為![]() ,當
,當![]() 時,重疊部分為△AOC,求出△AOC的面積即可,當
時,重疊部分為△AOC,求出△AOC的面積即可,當![]() 時,
時,![]() 平移
平移![]() 秒到
秒到![]() 的位置,
的位置,![]() 交
交![]() 于點
于點![]() ,如圖,重疊部分為四邊形
,如圖,重疊部分為四邊形![]() ,根據(jù)
,根據(jù)![]() 結合相似三角形的性質(zhì)可表示出
結合相似三角形的性質(zhì)可表示出![]() 的長,再根據(jù)四邊形
的長,再根據(jù)四邊形![]() 的面積=
的面積=![]() 的面積-
的面積-![]() 的面積即可求出
的面積即可求出![]() 關于
關于![]() 的函數(shù)關系式;
的函數(shù)關系式;
(3)①過點![]() 作
作![]() 軸于點
軸于點![]() ,交
,交![]() 于點
于點![]() ,利用點P、D的坐標表示出DN、NQ的長,再根據(jù)平行得
,利用點P、D的坐標表示出DN、NQ的長,再根據(jù)平行得![]() ,結合
,結合![]() 列出方程求解即可;
列出方程求解即可;
②當點P在第一象限時,過點P作PG⊥x軸于點G,易證△PGF∽△COA,故可設PG=4k,FG=3k,由勾股定理得PF=5k,由菱形得AF=PF=5k,故可表示出點P坐標,將點P坐標代入拋物線函數(shù)關系式列出方程求解即可,當點P在第四象限時,同理可得點P坐標.
解:(1)![]() ,
,
當![]() 時,
時,![]() ,解得
,解得![]() ,
,
∵點![]() 在點
在點![]() 的左側,
的左側,
∴![]() ,
,
∵![]() ,即
,即![]() ,
,
∴![]() ,
,
設直線![]() 的函數(shù)表達式為
的函數(shù)表達式為![]() ,
,
∵直線![]() 過點
過點![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() ,
,
當![]() 時,
時,![]() ,
,
∴![]() .
.
(2)當![]() 時,
時,![]() ,
,
解得:![]() ,
,
∵點![]() 在拋物線對稱軸的右側,
在拋物線對稱軸的右側,
∴ ![]() ,
,
∴![]() ,
,
∴![]() ,
,
當![]() 時,
時,
![]() ,
,
當![]() 時,
時,![]() 平移
平移![]() 秒到
秒到![]() 的位置,
的位置,![]() 交
交![]() 于點
于點![]() ,如圖,
,如圖,
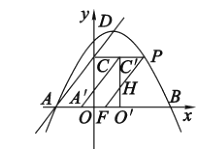
則![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即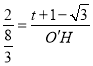 ,
,
∴![]() ,
,
∴![]()
![]()
![]()
![]()
=![]()
![]() .
.
綜上所述,當![]() 時,
時,![]() ;
;
當![]() 時,
時,![]() ;
;
(3)①如圖,過點![]() 作
作![]() 軸于點
軸于點![]() ,交
,交![]() 于點
于點![]() .
.
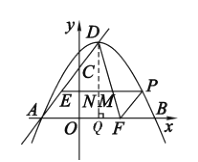
∵點![]() 的橫坐標為
的橫坐標為![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
∵![]() 軸,
軸,
∴![]() ,
,
當![]() 時,
時,![]() ,
,
∴![]() ,即
,即![]() ,
,
當![]() 時,
時,
![]() ,
,
∵點![]() 在拋物線對稱軸的右側,
在拋物線對稱軸的右側,
∴![]() ;
;
當![]() 時,
時,
![]() ,
,
∵點![]() 在拋物線對稱軸的右側,
在拋物線對稱軸的右側,
∴![]() ,
,
綜上所述,![]() 或
或![]() ,
,
②如圖,當點P在第一象限時,過點P作PG⊥x軸于點G,
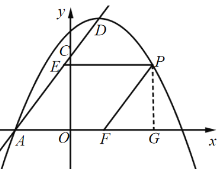
∵PF∥AC,
∴∠PFG=∠CAO
又∵∠PGF=∠COA=90°,
∴△PGF∽△COA,
∴![]() ,
,
∴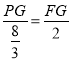 ,
,
∴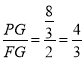 ,
,
∴設PG=4k,FG=3k,則PF=5k,
∵四邊形![]() 是菱形
是菱形
∴AF=PF=5k,
又∵點A(-2,0),
∴點P(-2+8k,4k)
∵點P在拋物線![]() 的圖像上,
的圖像上,
∴![]() ,
,
整理得![]()
解得![]() (舍去)
(舍去)
∴![]()
∴點P的坐標為![]() ,
,
如圖,當點P在第四象限時,過點P作PK⊥x軸于點K,
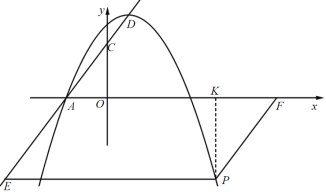
∵PF∥AC,
∴∠PFK=∠CAO,
又∵∠PKF=∠COA=90°,
∴△PKF∽△COA,
∴![]() ,
,
∴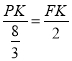 ,
,
∴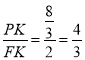 ,
,
∴設PK=4a,FK=3a,則PF=5a,
∵四邊形![]() 是菱形
是菱形
∴AF=PF=5a,
又∵點A(-2,0),
∴點P(-2+2a,-4a)
∵點P在拋物線![]() 的圖像上,
的圖像上,
∴![]() ,
,
整理得![]()
解得![]() (舍去)
(舍去)
∴![]()
∴點P的坐標為![]() ,
,
綜上所述,存在![]() ,使四邊形
,使四邊形![]() 是菱形,此時點
是菱形,此時點![]() 的坐標為
的坐標為![]() .
.


 期末沖刺100分創(chuàng)新金卷完全試卷系列答案
期末沖刺100分創(chuàng)新金卷完全試卷系列答案科目:初中數(shù)學 來源: 題型:
【題目】如圖是拋物線y=ax2+bx+c(a≠0)的部分圖象,其頂點坐標為(1,n),且與x軸的一個交點在點(3,0)和(4,0)之間,則下列結論:①4a﹣2b+c>0;②3a+b>0;③b2=4a(c﹣n);④一元二次方程ax2+bx+c=n﹣1有兩個互異實根.其中正確結論的個數(shù)是( )
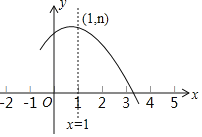
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】(12分)如圖,大樓AN上懸掛一條幅AB,小穎在坡面D處測得條幅頂部A的仰角為30°,沿坡面向下走到坡腳E處,然后向大樓方向繼續(xù)行走10米來到C處,測得條幅的底部B的仰角為45°,此時小穎距大樓底端N處20米.已知坡面DE=20米,山坡的坡度i=1:![]() (即tan∠DEM=1:
(即tan∠DEM=1:![]() ),且D、M、E、C、N、B、A在同一平面內(nèi),E、C、N在同一條直線上,求條幅的長度(結果精確到1米)(參考數(shù)據(jù):
),且D、M、E、C、N、B、A在同一平面內(nèi),E、C、N在同一條直線上,求條幅的長度(結果精確到1米)(參考數(shù)據(jù):![]() ≈1.73,
≈1.73,![]() ≈1.41)
≈1.41)
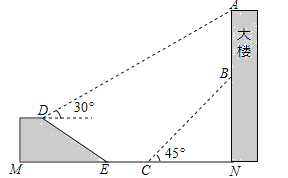
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=4,以AB為直徑的⊙O交BC于點D,交AC于點E,點P是AB的延長線上一點,且∠PDB=![]() ∠A,連接DE,OE.
∠A,連接DE,OE.
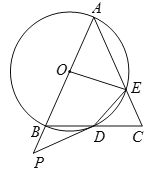
(1)求證:PD是⊙O的切線.
(2)填空:①當∠P的度數(shù)為______時,四邊形OBDE是菱形;
②當∠BAC=45°時,△CDE的面積為_________.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,已知反比例函數(shù)![]() 的圖象與一次函數(shù)
的圖象與一次函數(shù)![]() 的圖象在第一象限交于
的圖象在第一象限交于![]() 兩點,一次函數(shù)的圖象與
兩點,一次函數(shù)的圖象與![]() 軸交于點
軸交于點![]() .
.
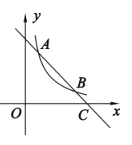
(1)求反比例函數(shù)和一次函數(shù)的表達式;
(2)當![]() 為何值時,
為何值時,![]() ?
?
(3)已知點![]() ,過點
,過點![]() 作
作![]() 軸的平行線,在第一象限內(nèi)交一次函數(shù)
軸的平行線,在第一象限內(nèi)交一次函數(shù)![]() 的圖象于點
的圖象于點![]() ,交反比例函數(shù)
,交反比例函數(shù)![]() 的圖象于點
的圖象于點![]() .結合函數(shù)圖象直接寫出當
.結合函數(shù)圖象直接寫出當![]() 時
時![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
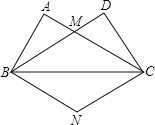
【題目】如圖,在△ABC和△DCB中,AB=DC,∠A=∠D,AC、DB交于點M.
(1)求證:△ABC≌△DCB;
(2)作CN∥BD,BN∥AC,CN交BN于點N,四邊形BNCM是什么四邊形?請證明你的結論.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,EF,EB是⊙O的弦,且EF=EB,EF與AB交于點C,連接OF,若∠AOF=40°,則∠F的度數(shù)是( )
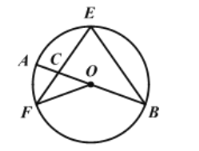
A.20°B.35°C.40°D.55°
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】下列說法正確的是 ( )
A.要調(diào)查現(xiàn)在人們在數(shù)學化時代的生活方式,宜采用普查方式
B.一組數(shù)據(jù)3,4,4,6,8,5的中位數(shù)是4
C.必然事件的概率是100%,隨機事件的概率大于0而小于1
D.若甲組數(shù)據(jù)的方差![]() =0.128,乙組數(shù)據(jù)的方差
=0.128,乙組數(shù)據(jù)的方差![]() =0.036,則甲組數(shù)據(jù)更穩(wěn)定
=0.036,則甲組數(shù)據(jù)更穩(wěn)定
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com