
【題目】如圖1,AD為正△ABC的高.
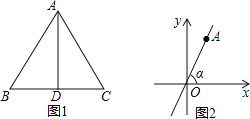
(1)利用此圖形填表:
30° | 60° | |
sin | ||
cos | ||
tan |
(2)利用(1)題中結(jié)論,計(jì)算:(![]() )﹣1﹣3tan60°+
)﹣1﹣3tan60°+![]()
(3)利用(1)題中結(jié)論解答:如圖2,直線l:y=![]() x與x軸所夾的銳角為α,直線l上點(diǎn)A的橫坐標(biāo)為1,求∠α.
x與x軸所夾的銳角為α,直線l上點(diǎn)A的橫坐標(biāo)為1,求∠α.
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;(從左向右排列)(2)2;(3)∠α=60°.
;(從左向右排列)(2)2;(3)∠α=60°.
【解析】
試題分析:(1)設(shè)△ABC的邊長(zhǎng)為2a,如圖1,根據(jù)等邊三角形的性質(zhì)得到∠BAD=30°,BD=a,再利用勾股定理計(jì)算出AD=![]() a,然后根據(jù)銳角三角函數(shù)的定義求30°和60°的銳角三角函數(shù)值;
a,然后根據(jù)銳角三角函數(shù)的定義求30°和60°的銳角三角函數(shù)值;
(2)根據(jù)負(fù)整數(shù)指數(shù)冪和特殊角的三角函數(shù)值得到原式=2﹣3![]() +3
+3![]() ,然后合并即可;
,然后合并即可;
(3)作AB⊥x軸于B,如圖2,利用一次函數(shù)圖象上點(diǎn)的坐標(biāo)特征求出A(1,![]() ),則OB=1,AB=
),則OB=1,AB=![]() ,再計(jì)算出∠α的正切值,然后根據(jù)特殊角的三角函數(shù)值得到∠α的度數(shù).
,再計(jì)算出∠α的正切值,然后根據(jù)特殊角的三角函數(shù)值得到∠α的度數(shù).
解:(1)設(shè)△ABC的邊長(zhǎng)為2a,如圖1,
∵AD⊥BC,
∴∠BAD=30°,BD=a,
∴AD=![]() =
=![]() a,
a,
∴sin∠BAD=sin30°=![]() =
=![]() =
=![]() ,則cosB=cos60°=
,則cosB=cos60°=![]() ;
;
cos∠BAD=cos30°=![]() =
=![]() =
=![]() ,則sinB=sin60°=
,則sinB=sin60°=![]() ;
;
tan∠BAD=tan30°=![]() =
=![]() =
=![]() ,則tanB=tan60°=
,則tanB=tan60°=![]() =
=![]() =
=![]() ;
;
故答案為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;(從左向右排列)
;(從左向右排列)
(2)原式=2﹣3![]() +3
+3![]()
=2;
(3)作AB⊥x軸于B,如圖2,
當(dāng)x=1時(shí),y=![]() x=
x=![]() ,則A(1,
,則A(1,![]() ),
),
∴OB=1,AB=![]() ,
,
在Rt△AOB中,tanα=![]() =
=![]() ,
,
∴∠α=60°.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】今年4月,全國(guó)山地越野車大賽在我市某區(qū)舉行,其中8名選手某項(xiàng)得分如表:
得分 | 80 | 85 | 87 | 90 |
人數(shù) | 1 | 3 | 2 | 2 |
則這8名選手得分的眾數(shù)、中位數(shù)分別是( )
A. 85,85 B. 87,85 C. 85,86 D. 85,87
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AB=5,AC=6,BC=7,點(diǎn)D,E分別在AB,AC上,DE∥BC.
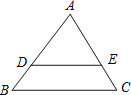
(1)當(dāng)AD:DB=4:3時(shí),求DE長(zhǎng);
(2)當(dāng)△ADE的周長(zhǎng)與四邊形BCED的周長(zhǎng)相等,求DE的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知長(zhǎng)方體的體積是1620,它的長(zhǎng)、寬、高的比是5:4:3,問長(zhǎng)方體的長(zhǎng)、寬、高是無理數(shù)嗎?為什么?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分線交BC于點(diǎn)M,交AB于點(diǎn)E,AC的垂直平分線交BC于點(diǎn)N,交AC于點(diǎn)F,則MN的長(zhǎng)為( )
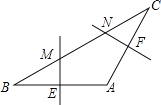
A.4cm B.3cm C.2cm D.1cm
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】若一個(gè)三角形三個(gè)內(nèi)角度數(shù)的比為2:7:4,那么這個(gè)三角形是( )
A. 直角三角形 B. 銳角三角形 C. 鈍角三角形 D. 等邊三角形
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com