
【題目】如圖,在△ABC中,AB=AC,點D、E、F分別在AB、BC、AC邊上,且BE=CF,BD=CE.
(1)求證:△DEF是等腰三角形;
(2)當∠A=50°時,求∠DEF的度數.

【答案】(1)證明見解析;(2)65°
【解析】試題分析:⑴由AB=AC,可知∠B=∠ C,根據題意易得△ BDE ≌ △ CEF(SAS),從而得到DE=EF,命題得證.
⑵因為∠ A=50°,所以∠ B=∠ C=65°,由⑴可知,∠BDE=∠CEF,所以∠DEB+∠CEF=
∠DEB+∠ BDE=115°,從而∠ DEF=180°-115°=65°.
試題解析:⑴∵ AB=AC,∴ ∠B=∠ C.
在△ BDE和△ CEF中,
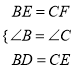 ,
,
∴ △ BDE ≌ △ CEF(SAS),則DE=EF,故△ DEF是等腰三角形.
⑵在△ABC中,∵∠A=50°,∴∠B=∠C=65°.
∵ △ BDE ≌ △ CEF,∴ ∠BDE=∠CEF,
∴ ∠DEB+∠CEF=∠DEB+∠ BDE=180°-65°=115°,
則 ∠ DEF=180°-(∠DEB+∠CEF)=180°-115°=65°.


科目:初中數學 來源: 題型:
【題目】在檢測一批剛出廠的足球的質量時,隨機抽取了4個足球來測量其質量,把超過標準質量的克數記為正數,不足標準質量的克數記為負數,檢測結果如下表:
足球的編號 | 1 | 2 | 3 | 4 |
與標準質量的差(克) | +3 | +2 | ﹣1 | ﹣2 |
則生產較合格的足球的編號是( )
A.1號B.2號C.3號D.4號
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校準備購進一批節能燈,已知1只A型節能燈和3只B型節能燈共需26元;3只A型節能燈和2只B型節能燈共需29元.
(1)求一只A型節能燈和一只B型節能燈的售價各是多少元;
(2)學校準備購進這兩種型號的節能燈共50只,并且A型節能燈的數量不多于B型節能燈數量的3倍,問A型節能燈最多可以買多少只?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個口袋中有紅球、白球共10個,這些球除顏色外都相同.將口袋中的球攪拌均勻,從中隨機摸出一個球,記下它的顏色后再放回口袋中,不斷重復這一過程,共摸了100次球,發現有70次摸到紅球.請你估計這個口袋中有_____個白球.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市準備購進A、B兩種品牌臺燈,其中A每盞進價比B進價貴30元,A售價120元,B售價80元.已知用1040元購進的A數量與用650元購進B的數量相同.
(1)求A、B的進價;
(2)超市打算購進A、B臺燈共100盞,要求A、B的總利潤不得少于3400元,不得多于3550元,問有多少種進貨方案?
(3)在(2)的條件下,該超市決定對A進行降價促銷,A臺燈每盞降價m(8<m<15)元,B不變,超市如何進貨獲利最大?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在學習“有理數加法“時,我們利用“(+5)+(+3)=+8,(-5)+(-3)=-8,……”抽象歸納推出了“同號兩數相加,取相同的符號,并把絕對值相加”的加法法則.這種推導方法叫( )
A.排除法B.歸納法C.類比法D.數形結合法
查看答案和解析>>
科目:初中數學 來源: 題型:
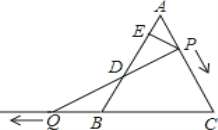
【題目】如圖,△ABC是邊長為6的等邊三角形,P是AC邊上一動點,由A向C運動(與A、C不重合),Q是CB延長線上一點,與點P同時以相同的速度由B向CB延長線方向運動(Q不與B重合),過P作PE⊥AB于E,連接PQ交AB于D.
(1)當∠BQD=30°時,求AP的長;
(2)證明:在運動過程中,點D是線段PQ的中點;
(3)當運動過程中線段ED的長是否發生變化?如果不變,求出線段ED的長;如果變化請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com