
【題目】如圖,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分別交AD、DE于點G、F,AC與DE交于點H.求證: 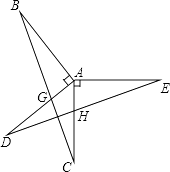
(1)△ABC≌△ADE;
(2)BC⊥DE.
【答案】
(1)證明:∵AB⊥AD,AC⊥AE,
∴∠DAB=∠CAE=90°,
∴∠DAB+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE,
在△ABC和△ADE中,
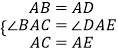
∴△ABC≌△ADE(SAS)
(2)證明:∵△ABC≌△ADE,
∴∠E=∠C,
∵∠E+∠AHE=90°,∠AHE=∠DHC,
∴∠C+∠DHC=90°,
∴BC⊥DE
【解析】(1)利用AB⊥AD,AC⊥AE,得出∠DAB=∠CAE,進一步得出∠BAC=∠DAE,再根據已知條件及全等的判定方法SAS即可證得△ABC≌△ADE;(2)由△ABC≌△ADE,得出∠E=∠C,利用∠E+∠AHE=90°,推出∠C+∠DHC=90°,結論成立.


科目:初中數學 來源: 題型:
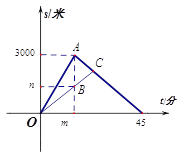
【題目】小明和爸爸周末到濕地公園進行鍛煉,兩人上午9:00從公園入口出發,沿相同路線勻速運動,小明15分鐘后到達目的地,此時爸爸距出發地1200米,小明到達目的地后立即按原路勻速返回,與爸爸相遇后,和爸爸一起從原路返回出發地.小明、爸爸在鍛煉過程中離出發地的路程與小明出發的時間的函數關系如圖.
(1)圖中![]() ,
, ![]() ;
;
(2)求小明和爸爸相遇的時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有理數a,b在數軸上的表示如圖所示,則下列結論中: ①ab<0, ②![]() <0,③a+b<0,④a-b<0,⑤a<|b|,⑥-a>-b,正確的有( )
<0,③a+b<0,④a-b<0,⑤a<|b|,⑥-a>-b,正確的有( )
![]()
A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知某種禮炮的升空高度h(m)與飛行時間t(s)的關系式是h=﹣(t﹣4)2+20.若此禮炮在升空到最高處時引爆,則引爆需要的時間為( )
A.3sB.4sC.5sD.6s
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形OABC的頂點A在y軸上,C在x軸上,雙曲線y=![]() 與AB交于點D,與BC交于點E,DF⊥x軸于點F,EG⊥y軸于點G,交DF于點H.若矩形OGHF和矩形HDBE的面積分別是1和2,則k的值為( )
與AB交于點D,與BC交于點E,DF⊥x軸于點F,EG⊥y軸于點G,交DF于點H.若矩形OGHF和矩形HDBE的面積分別是1和2,則k的值為( )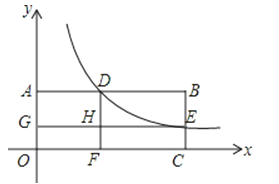
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某花園的護欄都是用直徑![]() 的半圓形條鋼組制而成,且每增加一個半圓形條鋼,半圓護欄長度增加
的半圓形條鋼組制而成,且每增加一個半圓形條鋼,半圓護欄長度增加![]() ,(
,( ![]() )設半圓形條鋼的總個數為
)設半圓形條鋼的總個數為![]() (
(![]() 為正整數),護欄總長為
為正整數),護欄總長為![]() .
.
(![]() )當
)當![]() 時,用
時,用![]() 的代數式表示
的代數式表示![]() .
.
(![]() )若護欄總長度為
)若護欄總長度為![]() ,當
,當![]() 時,所用半圓形條鋼的個數.
時,所用半圓形條鋼的個數.
(![]() )若護欄的總長度不變,則當
)若護欄的總長度不變,則當![]() 時,用了
時,用了![]() 個半圓形條鋼,當
個半圓形條鋼,當![]() 時,用了
時,用了![]() 個半圓形條鋼,請用含
個半圓形條鋼,請用含![]() 的代數式表示
的代數式表示![]() .
.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料:
小丁在研究數學問題時遇到一個定義:對于排好順序的三個數: ![]() ,稱為數列
,稱為數列![]() .計算
.計算![]() ,
, ![]() ,
, ![]() 將這三個數的最小值稱為數列
將這三個數的最小值稱為數列![]() 的價值.例如,對于數列2,﹣1,3,因為
的價值.例如,對于數列2,﹣1,3,因為![]() ,
, ![]() ,
, ![]() ,所以數列2,﹣1,3的價值為
,所以數列2,﹣1,3的價值為![]() .
.
小丁進一步發現:當改變這三個數的順序時,所得到的數列都可以按照上述方法計算其相應的價值.如數列﹣1,2,3的價值為![]() ;數列3,﹣1,2的價值為1;….經過研究,小丁發現,對于“2,﹣1,3”這三個數,按照不同的排列順序得到的不同數列中,價值的最小值為
;數列3,﹣1,2的價值為1;….經過研究,小丁發現,對于“2,﹣1,3”這三個數,按照不同的排列順序得到的不同數列中,價值的最小值為![]() .根據以上材料,回答下列問題:
.根據以上材料,回答下列問題:
(1)數列﹣4,﹣3,2的價值為 ;
(2)將“﹣4,﹣3,2”這三個數按照不同的順序排列,可得到若干個數列,這些數列的價值的最小值為 ,取得價值最小值的數列為 (寫出一個即可);
(3)將2,﹣9,a(a>1)這三個數按照不同的順序排列,可得到若干個數列.若這些數列的價值的最小值為1,則a的值為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com