
【題目】如圖,在正方形ABCD中,點E、F分別是BC、CD的中點,DE交AF于點M,點N為DE的中點. 
(1)若AB=4,求△DNF的周長及sin∠DAF的值;
(2)求證:2ADNF=DEDM.
【答案】
(1)解:∵點E、F分別是BC、CD的中點,
∴EC=DF= ![]() ×4=2,
×4=2,
由勾股定理得,DE= ![]() =2
=2 ![]() ,
,
∵點F是CD的中點,點N為DE的中點,
∴DN= ![]() DE=
DE= ![]() ×2
×2 ![]() =
= ![]() ,
,
NF= ![]() EC=
EC= ![]() ×2=1,
×2=1,
∴△DNF的周長=1+ ![]() +2=3+
+2=3+ ![]() ;
;
在Rt△ADF中,由勾股定理得,AF= ![]() =
= ![]() =2
=2 ![]() ,
,
所以,sin∠DAF= ![]() =
= ![]() =
= ![]()
(2)證明:在△ADF和△DCE中,
 ,
,
∴△ADF≌△DCE(SAS),
∴AF=DE,∠DAF=∠CDE,
∵∠DAF+∠AFD=90°,
∴∠CDE+∠AFD=90°,
∴AF⊥DE,
∵點N、F分別是DE、CD的中點,
∴NF是△CDE的中位線,
∴DF=EC=2NF,
∵cos∠DAF= ![]() ,
,
cos∠CDE= ![]() ,
,
∴ ![]() ,
,
∴2ADNF=DEDM.
【解析】(1)根據線段中點定義求出EC=DF=2,再利用勾股定理列式求出DE,然后三角形的中位線平行于第三邊并且等于第三邊的一半求出NF,再求出DN,再根據三角形的周長的定義列式計算即可得解;利用勾股定理列式求出AF,再根據銳角的正弦等于對邊比斜邊列式計算即可得解;(2)利用“邊角邊”證明△ADF和△DCE全等,根據全等三角形對應邊相等可得AF=DE,全等三角形對應角相等可得∠DAF=∠CDE,再求出AF⊥DE,然后根據三角形的中位線平行于第三邊并且等于第三邊的一半可得DF=EC=2NF,然后根據∠DAF和∠CDE的余弦列式整理即可得證.
【考點精析】認真審題,首先需要了解正方形的性質(正方形四個角都是直角,四條邊都相等;正方形的兩條對角線相等,并且互相垂直平分,每條對角線平分一組對角;正方形的一條對角線把正方形分成兩個全等的等腰直角三角形;正方形的對角線與邊的夾角是45o;正方形的兩條對角線把這個正方形分成四個全等的等腰直角三角形),還要掌握相似三角形的判定與性質(相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等于相似比;相似三角形周長的比等于相似比;相似三角形面積的比等于相似比的平方)的相關知識才是答題的關鍵.


 挑戰100單元檢測試卷系列答案
挑戰100單元檢測試卷系列答案科目:初中數學 來源: 題型:
【題目】方成同學看到一則材料,甲開汽車,乙騎自行車從M地出發沿一條公路勻速前往N地,設乙行駛的時間為t(h),甲乙兩人之間的距離為y(km),y與t的函數關系如圖1所示,方成思考后發現了圖1的部分正確信息,乙先出發1h,甲出發20分鐘后與乙相遇,…,請你幫助方成同學解決以下問題: 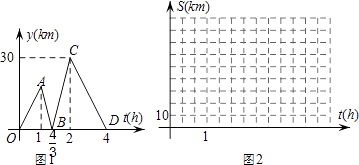
(1)分別求出線段BC,CD所在直線的函數表達式;
(2)當15<y<25時,求t的取值范圍;
(3)分別求出甲、乙行駛的路程S甲、S乙與時間t的函數表達式,并在圖2所給的直角坐標系中分別畫出它們的圖象.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=AC,∠BAC=60°,點E為直線AC上一點,D為直線BC上的一點,且DA=DE. 當點D在線段BC上時,如圖①,易證:BD+AB=AE;
當點D在線段CB的延長線上時,如圖②、圖③,猜想線段BD,AB和AE之間又有怎樣的數量關系?寫出你的猜想,并選擇一種情況給予證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),拋物線y=﹣ ![]() x2+x+c與x軸交于A、B兩點,與y軸交于點C,其中點A的坐標為(﹣2,0).
x2+x+c與x軸交于A、B兩點,與y軸交于點C,其中點A的坐標為(﹣2,0).
(1)求此拋物線的解析式;
(2)①若點D是第一象限內拋物線上的一個動點,過點D作DE⊥x軸于E,連接CD,以OE為直徑作⊙M,如圖(2),試求當CD與⊙M相切時D點的坐標;
②點F是x軸上的動點,在拋物線上是否存在一點G,使A、C、G、F四點為頂點的四邊形是平行四邊形?若存在,求出點G的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學習委員統計全班50位同學對語文、數學、英語、體育、音樂五個科目最喜歡情況,所得數據用表格與條形圖描述如下:
科目 | 語文 | 數學 | 英語 | 體育 | 音樂 |
人數 | 10 | a | 15 | 3 | 2 |

(1)表格中a的值為;
(2)補全條形圖;
(3)小李是最喜歡體育之一,小張是最喜歡音樂之一,計劃從最喜歡體育、音樂的人中,每科目各選1人參加學校訓練,用列表或樹形圖表示所有結果,并求小李、小張至少有1人被選上的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c圖象如圖,下列正確的個數為( )
①bc>0;
②2a﹣3c<0;
③2a+b>0;
④ax2+bx+c=0有兩個解x1 , x2 , 當x1>x2時,x1>0,x2<0;
⑤a+b+c>0;
⑥當x>1時,y隨x增大而減小.
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某“愛心義賣”活動中,購進甲、乙兩種文具,甲每個進貨價高于乙進貨價10元,90元買乙的數量與150元買甲的數量相同.
(1)求甲、乙進貨價;
(2)甲、乙共100件,將進價提高20%進行銷售,進貨價少于2080元,銷售額要大于2460元,求有幾種方案?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com