
【題目】如圖,矩形ABCD中,AB=1,AD=2,E是AD中點,P在射線BD上運動,若△BEP為等腰三角形,則線段BP的長度等于 . 
【答案】![]() 或
或 ![]() 或
或 ![]()
【解析】解:∵矩形ABCD中,AB=1,AD=2,E是AD中點, ∴∠BAD=90°,AE=DE=1,
∴△ABE是等腰直角三角形,
∴BE= ![]() AB=
AB= ![]() .
.
若△BEP為等腰三角形,則分三種情況:①當BP=BE時,顯然BP= ![]() ;②當PB=PE時,如圖,連結AP.
;②當PB=PE時,如圖,連結AP.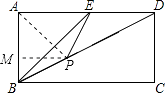
∵PB=PE,AB=AE,
∴AP垂直平分BE,
∵△ABE是等腰直角三角形,
∴∠BAP=∠EAP=45°.
作PM⊥AB于M,設PM=x,
∵S△ABD=S△ABP+S△APD
∴ ![]() ×1x+
×1x+ ![]() ×2x=
×2x= ![]() ×1×2,
×1×2,
解得x= ![]() ,
,
∴PM= ![]() ,
,
∴BP= ![]() =
= ![]() =
= ![]() ;③當EB=EP時,如圖,過A作AF⊥BD于F,
;③當EB=EP時,如圖,過A作AF⊥BD于F,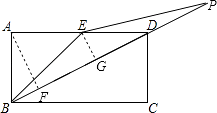
過E作EG⊥BD于G.
在Rt△ABF中,AF=ABsin∠ABF=1× ![]() =
= ![]() ,
,
∵AE=ED,EG∥AF,
∴EG= ![]() AF=
AF= ![]() .
.
在Rt△BEG中,∵BE= ![]() ,EG=
,EG= ![]() ,
,
∴BG= ![]() =
= ![]() .
.
∵EB=EP,EG⊥BP,
∴BP=2BG= ![]() .
.
綜上所述,線段BP的長度等于 ![]() 或
或 ![]() 或
或 ![]() .
.
故答案為 ![]() 或
或 ![]() 或
或 ![]() .
.
先根據矩形的性質及中點的定義得出∠BAD=90°,AE=DE=1,那么△ABE是等腰直角三角形,BE= ![]() AB=
AB= ![]() .再分三種情況討論:①BP=BE;②PB=PE;③EB=EP.
.再分三種情況討論:①BP=BE;②PB=PE;③EB=EP.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】某校在踐行“社會主義核心價值觀”演講比賽中,對名列前20名的選手的綜合分數m進行分組統計,結果如表所示:
組號 | 分組 | 頻數 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |
(1)求a的值;
(2)若用扇形圖來描述,求分數在8≤m<9內所對應的扇形圖的圓心角大小;
(3)將在第一組內的兩名選手記為:A1、A2 , 在第四組內的兩名選手記為:B1、B2 , 從第一組和第四組中隨機選取2名選手進行調研座談,求第一組至少有1名選手被選中的概率(用樹狀圖或列表法列出所有可能結果). 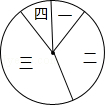
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】微信運動和騰訊公益推出了一個愛心公益活動:一天中走路步數達到10000步及以上可通過微信運動和騰訊基金會向公益活動捐款,如果步數在10000步及以上,每步可捐0.0002元;若步數在10000步以下,則不能參與捐款.
(1)老趙某天的步數為13000步,則他當日可捐多少錢?
(2)已知甲、乙、丙三人某天通過步數共捐了8.4元,且甲的步數=乙的步數=丙步數的3倍,則丙走了多少步?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解
如圖(1),在正多邊形A1A2A3…An的邊A2A3上任取一不與點A2重合的點B2 , 并以線段A1B2為邊在線段A1A2的上方作以正多邊形A1B2B3…Bn , 把正多邊形A1B2B3…Bn叫正多邊形A1A2…An的準位似圖形,點A3稱為準位似中心.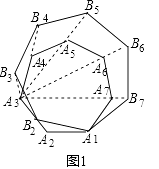
特例論證
(1)如圖(2)已知正三角形A1A2A3的準位似圖形為正三角形A1B2B3 , 試證明:隨著點B2的運動,∠B3A3A1的大小始終不變.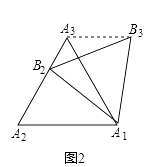
(2)如圖(3)已知正方形A1A2A3A4的準位似圖形為正方形A1B2B3B4 , 隨著點B2的運動,∠B3A3A4的大小始終不變?若不變,請求出∠B3A3A4的大小;若改變,請說明理由.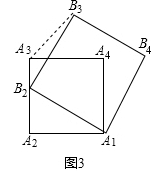
(3)在圖(1)的情況下:
①試猜想∠B3A3A4的大小是否會發生改變?若不改變,請用含n的代數式表示出∠B3A3A4的大小(直接寫出結果);若改變,請說明理由.
①∠B3A3A4+∠B4A4A5+∠B5A5A6+…+∠BnAnA1= ![]() (用含n的代數式表示)
(用含n的代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC三個頂點的坐標分別為A(1,1),B(4,2),C(3,4).
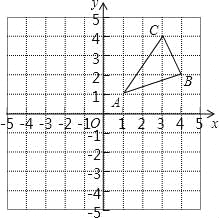
(1)請畫出△ABC向左平移5個單位長度后得到的△A1B1C1;
(2)請畫出△ABC關于原點對稱的△A2B2C2;
(3)在x軸上求作一點P,使△PAB的周長最小,請畫出△PAB,并直接寫出P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示是某一蓄水池的排水速度![]() h)與排完水池中的水所用的時間t(h)之間的函數關系圖象.
h)與排完水池中的水所用的時間t(h)之間的函數關系圖象.
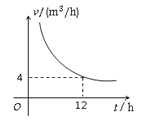
(1)請你根據圖象提供的信息求出此蓄水池的蓄水量;
(2)寫出此函數的解析式;
(3)若要6 h排完水池中的水,那么每小時的排水量應該是多少?
(4)如果每小時排水量是![]() ,那么水池中的水要用多少小時排完?
,那么水池中的水要用多少小時排完?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司要把240噸白砂糖運往某市的A、B兩地,用大小兩種貨車共20輛,恰好能一次性裝完這批白砂糖.已知這兩種大小貨車的載重分別是15噸/輛和10噸/輛,運往A地的運費為:大車630元/輛,小車420元/輛;運往B地的運費為:大車750元/輛,小車550元/輛.
(1)求大小兩種貨車各多少輛.
(2)如果安排10輛貨車前往A地,其中調往A地的大貨車有a輛,其余貨車前往B地,填寫下表:
前往A地 | 前往B地 | |
大貨車/輛 | a | |
小貨車/輛 |
(3)按照上表的分配方案,若設總費用為W,求W與a的關系式(用含a的代數式表示W)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com