
【題目】如圖,直線y![]() x4與 x軸、y軸的交點為A,B.按以下步驟作圖:
x4與 x軸、y軸的交點為A,B.按以下步驟作圖:
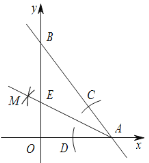
①以點 A 為圓心,適當長度為半徑作弧,分別交 AB,x 軸于點 C,D;
②分別以點 C,D 為圓心,大于![]() CD的長為半徑作弧,兩弧在∠OAB內交于點M;③作射線AM,交 y 軸于點E.則點 E 的坐標為____________
CD的長為半徑作弧,兩弧在∠OAB內交于點M;③作射線AM,交 y 軸于點E.則點 E 的坐標為____________
【答案】(0,![]() )
)
【解析】
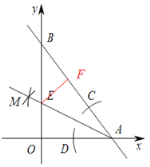
過點E作EF⊥AB于F,根據直線解析式求出A、B的坐標,根據勾股定理得AB=5,再通過證明△OAE≌△FAE,可得OA=AF=3,故BF=AB-AF=2,設OE=x,則EF=x,BE=4-x,根據勾股定理列方程求解即可.
解:過點E作EF⊥AB于F,如圖所示,
在y![]() x4中,當x=0時,y=4;當y=0時,x=3,
x4中,當x=0時,y=4;當y=0時,x=3,
即A(3,0),B(0,4),
在Rt△AOB中,由勾股定理得:AB=5,
由題意的尺規作圖方法可知,AM為∠BOA的平分線,
∴EO=EF,
∴△OAE≌△FAE,
∴OA=AF=3,
∴BF=AB-AF=2,
設OE=x,則EF=x,BE=4-x,
在Rt△BEF中,由勾股定理得:
(4-x)2=x2+22,
解得:x=![]() ,即OE=
,即OE=![]() ,
,
∴答案為:(0,![]() ).
).


科目:初中數學 來源: 題型:
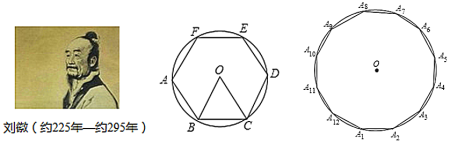
【題目】劉徽計算圓周率是從正六邊形開始的,易知圓的內接正六邊形可分為六個全等的正三角形,每個三角形的邊長均為圓的半徑![]() .此時圓內接正六邊形的周長為
.此時圓內接正六邊形的周長為![]() ,如果將圓內接正六邊形的周長等同于圓的周長,可得圓周率為3.當正十二邊形內接于圓時,如果按照上述方法計算,可得圓周率為______.(參考數據:
,如果將圓內接正六邊形的周長等同于圓的周長,可得圓周率為3.當正十二邊形內接于圓時,如果按照上述方法計算,可得圓周率為______.(參考數據:![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+c經過點(﹣1,0),對稱軸是x=1,現有結論:①abc>0 ②9a﹣3b+c=0 ③b=﹣2a④(![]() ﹣1)b+c<0,其中正確的有( )
﹣1)b+c<0,其中正確的有( )

A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數![]() 的圖象與
的圖象與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,直線
,直線![]() 經過點
經過點![]() .
.
(1)求![]() 的值;
的值;
(2)若點![]() 是直線
是直線![]() 上方拋物線的一部分上的動點,過點P作
上方拋物線的一部分上的動點,過點P作![]() 軸于點F,交直線AB于點D,求線段
軸于點F,交直線AB于點D,求線段![]() 的最大值
的最大值
(3)在(2)的條件下,連接![]() ,點
,點![]() 是拋物線對稱軸上的一動點,在拋物線上是否存在點
是拋物線對稱軸上的一動點,在拋物線上是否存在點![]() ,使得以
,使得以![]() 為頂點的四邊形是平行四邊形,若存在,請直接寫出點
為頂點的四邊形是平行四邊形,若存在,請直接寫出點![]() 的坐標,若不存在,請說明理由.
的坐標,若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
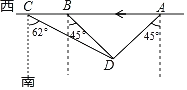
【題目】如圖,某海監船向正西方向航行,在A處望見一艘正在作業的漁船D在南偏西45°方向,海監船航行到B處時,望見漁船D在南偏東45°方向,又航行半小時到達C處望見漁船D在南偏東62°方向,若海監船的速度為40海里/小時,求A、B之間的距離.(精確到0.1海里,參考數據:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
查看答案和解析>>
科目:初中數學 來源: 題型:
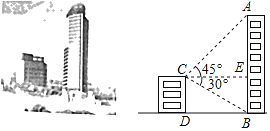
【題目】如圖,某校數學興趣小組的小明同學為測量位于玉溪大河畔的云銅礦業大廈AB的高度,小明在他家所在的公寓樓頂C處測得大廈頂部A處的仰角為45°,底部B處的俯角為30°.已知公寓高為40m,請你幫助小明計算公寓樓與礦業大廈間的水平距離BD的長度及礦業大廈AB的高度.(結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=x2﹣bx+c(b,c為常數,b>0)經過點A(﹣1,0),點M(m,0)是x軸正半軸上的動點.
(1)當b=2時,求拋物線的頂點坐標;
(2)點D(b,yD)在拋物線上,當AM=AD,m=3時,求b的值;
(3)點Q(b+![]() ,yQ)在拋物線上,當
,yQ)在拋物線上,當![]() AM+2
AM+2![]() QM的最小值為
QM的最小值為![]() 時,求b的值.(說明:yD表示D點的縱坐標,yQ表示Q點的縱坐標)
時,求b的值.(說明:yD表示D點的縱坐標,yQ表示Q點的縱坐標)
查看答案和解析>>
科目:初中數學 來源: 題型:
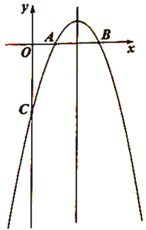
【題目】如圖,在平面直角坐標系中,拋物線![]() 與
與![]() 軸交于
軸交于![]() 和
和![]() ,與
,與![]() 軸交于點
軸交于點![]() .
.
(1)求該拋物線的解析式;
(2)繞點![]() 旋轉的直線
旋轉的直線![]() :
:![]() 與
與![]() 軸相交于點
軸相交于點![]() ,與拋物線相交于點
,與拋物線相交于點![]() ,且滿足
,且滿足![]() 時,求直線
時,求直線![]() 的解析式;
的解析式;
(3)點![]() 為拋物線上的一點,點
為拋物線上的一點,點![]() 為拋物線對稱軸上的一點,是否存在以點
為拋物線對稱軸上的一點,是否存在以點![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的平行四邊形,若存在,請直接寫出點
為頂點的平行四邊形,若存在,請直接寫出點![]() 的坐標:若不存在,請說明理由.
的坐標:若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com