【題目】某商品的進價為每件50元，售價為每件60元，每天可賣出190件；如果每件商品的售價每上漲1元，則每天少賣10件，設每件商品的售價上漲x元，每天的銷售利潤為y元．
（1）求y關于x的關系式；
（2）每件商品的售價定為多少元時，每天的利潤恰為1980元？
（3）每件商品的售價定為多少元時，每天可獲得最大利潤？最大利潤是多少元？
【答案】（1）y=﹣10x2+90x+1900；（2）每件商品的售價定為61元或68元時，每天的利潤恰為1980元；（3）每件商品的售價定為64.5元時，每天可獲得最大利潤，最大利潤是2102.5元．
【解析】試題分析：（1）利用銷量乘以每件利潤=總利潤得出關系式即可；
（2）利用（1）中所求關系式，進而使y=1980進而得出即可；
（3）利用配方法求出二次函數最值，結合x的取值范圍得出答案．
試題解析：（1）設每件商品的售價上漲x元，每天的銷售利潤為y元，
則y=（60﹣50+x）（190﹣10x）=﹣10x2+90x+1900；
（2）當y=1980，則1980=﹣10x2+90x+1900，
解得：x1=1，x2=8．
故每件商品的售價定為61元或68元時，每天的利潤恰為1980元；
（3）y=﹣10x2+90x+1900=﹣10（x﹣
）2+2102.5，
故當x=4.5時，y=2102.5（元），
即每件商品的售價定為64.5元時，每天可獲得最大利潤，最大利潤是2102.5元．
口算心算速算應用題系列答案
同步拓展閱讀系列答案科目：初中數學 來源： 題型：
【題目】如圖，一棵大樹在一次強臺風中折斷倒下，未折斷樹桿
與地面仍保持垂直的關系，而折斷部分
與未折斷樹桿
形成
的夾角．樹桿
旁有一座與地面垂直的鐵塔
，測得
米，塔高
米．在某一時刻的太陽照射下，未折斷樹桿
落在地面的影子
長為
米，且點
、
、
、
在同一條直線上，點
、
、
也在同一條直線上．求這棵大樹沒有折斷前的高度．（結果精確到
，參考數據： 
， 
， 
）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列四幅圖象近似刻畫兩個變量之間的關系，請按圖象順序將下面四種情景與之對應排序（ ）.
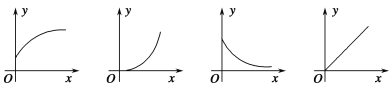
①一輛汽車在公路上勻速行駛（汽車行駛的路程與時間的關系）
②向錐形瓶中勻速注水（水面的高度與注水時間的關系）
③將常溫下的溫度計插入一杯熱水中（溫度計的讀數與時間的關系）
④一杯越來越涼的水（水溫與時間的關系）
A.①②④③ B.③④②①
C.①④②③ D.③②④①
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下列材料：
“
≥0”這個結論在數學中非常有用，有時我們需要將代數式配成完全平方式．例如： 
，
∵
≥0，
∴
≥1，
∴
≥1.
試利用“配方法”解決下列問題：
(1)填空： 
(x )2＋ ；
(2) 已知a，b，c是△ABC的三邊長，滿足a2+b2=10a+8b﹣41，且c是△ABC中最長的邊，求c的取值范圍．
(3)比較代數式
與
的大小．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，在△ABC中，AD平分∠BAC，AD⊥BC，垂足為D，AN是△ABC外角∠CAM的平分線，CE⊥AN，垂足為E.
（1）求證：四邊形ADCE是矩形；
（2）當△ABC滿足什么條件時，四邊形ADCE是正方形？給出證明.
查看答案和解析>>
科目：初中數學 來源： 題型：
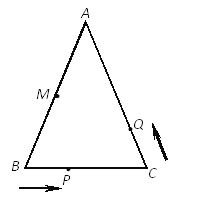
【題目】如圖，已知△ABC中，AB=AC=12厘米，（即∠B=∠C），BC=9厘米，點M為AB的中點，
（1）如果點P在線段BC上以2厘米/秒的速度由點B向點C運動，同時，點Q在線段CA上由點C向點A運動.
①若點Q的運動速度與點P的運動速度相等，經過1.5秒后，△BPM與△CQP是否全等？請說明理由.
②若點Q的運動速度與點P的運動速度不相等，當點Q的運動速度為多少時，能夠使△BPM與△CQP全等？
（2）若點Q以②中的運動速度從點C出發，點P以原來的運動速度從點B同時出發，都逆時針沿△ABC三邊運動，求經過多長時間點P與點Q第一次在△ABC的哪條邊上相遇？
查看答案和解析>>
科目：初中數學 來源： 題型：
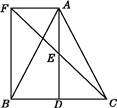
【題目】如圖，△ABC中，D是BC邊上的一點，E為AD的中點，過A作BC的平行線交CE的延長線于F，且AF=BD，連接BF.
(1)求證:BD=CD;
(2)如果AB=AC，試判斷四邊形AFBD的形狀，并證明你的結論.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在方格紙內將△ABC經過一次平移后得到△A′B′C′，圖中標出了點B的對應點B′．
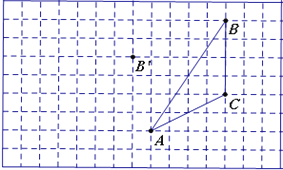
(1) 補全△A′B′C′；
(2) 根據下列條件，利用網格點和直尺畫圖：
畫出△ABC中：
①AC邊上的中線BD；
②AC邊上的高線BE；
(3)寫出△ABD的面積 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
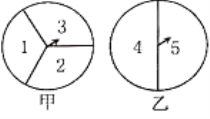
【題目】如圖，甲轉盤被分成3個面積相等的扇形、乙轉盤被分成2個面積相等的扇形．小夏和小秋利用它們來做決定獲勝與否的游戲．規定小夏轉甲盤一次、小秋轉乙盤一次為一次游戲（當指針指在邊界線上時視為無效，重轉）.
（1）小夏說：“如果兩個指針所指區域內的數之和為6或7，則我獲勝；否則你獲勝”.按小夏設計的規則，請你寫出兩人獲勝的可能性分別是多少?
（2）請你對小夏和小秋玩的這種游戲設計一種公平的游戲規則，并用一種合適的方法(例如：樹狀圖，列表)說明其公平性.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com