
【題目】如圖,△ABC中,AB=AC,∠BAC=90°,點D是直線AB上的一動點(不和A、B重合),BE⊥CD于E,交直線AC于F
(1)點D在邊AB上時,試探究線段BD、AB和AF的數量關系,并證明你的結論;
(2)點D在AB的延長線或反向延長線上時,(1)中的結論是否成立?若不成立,請寫出正確結論并證明。
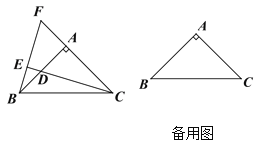
【答案】(1)AB=AF+BD,證明詳見解析;(2)不成立,點D在AB的延長線上時,AB=AF-BD;點D在AB的反向延長線上時,AB=BD-AF,證明詳見解析.
【解析】
(1)根據已知條件易證△FAB≌△DAC,由全等三角形的性質可得FA=DA,由此即可證得AB=AD+BD=FA+BD;(2)由于點D的位置在變化,因此線段AF、BD、AB之間的大小關系也會相應地發生變化,只需畫出圖象并借鑒(1)中的證明思路就可解決問題.
(1)AB=FA+BD.
證明:如圖,

∵BE⊥CD即∠BEC=90°,∠BAC=90°,
∴∠F+∠FBA=90°,∠F+∠FCE=90°.
∴∠FBA=∠FCE.
∵∠FAB=180°-∠DAC=90°,
∴∠FAB=∠DAC.
在△FAB和△DAC中,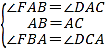 .
.
∴△FAB≌△DAC(ASA).
∴FA=DA.
∴AB=AD+BD=FA+BD.
(2)(1)中的結論不成立.
點D在AB的延長線上時,AB=AF-BD;點D在AB的反向延長線上時,AB=BD-AF.
理由如下:
點D在AB的延長線上時,如圖2.
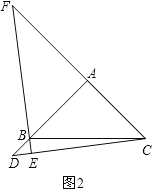
類比(1)的方法可得:FA=DA.
則AB=AD-BD=AF-BD.
②點D在AB的反向延長線上時,如圖3.
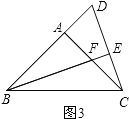
類比(1)的方法可得:FA=DA.
則AB=BD-AD=BD-AF.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中數學 來源: 題型:
【題目】已知數軸上三點M,O,N對應的數分別為﹣2,0,4,點P為數軸上任意一點,其對應的數為x.
(1)如果點P到點M點N的距離相等,則x= .
(2)數軸上是否存在點P,使點P到點M、點N的距離之和是10?若存在,求出x的值;若不存在,請說明理由.
(3)如果點P以每分鐘1個單位長度的速度從點O向左運動,同時點M和點N分別以每分鐘2個單位長度和每分鐘3個單位長度的速度也向左運動.設t分鐘時點P到點M、點N的距離相等,求t的值.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知BD垂直平分線段AC,∠BCD=∠ADF,AF⊥AC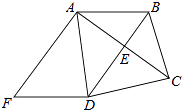
(1)證明:四邊形ABDF是平行四邊形;
(2)若AF=DF=5,AD=6,求AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知將一塊直角三角板DEF放置在△ABC上,使得該三角板的兩條直角邊DE,DF恰好分別經過點B、C.
(1)∠DBC+∠DCB= 度;
(2)過點A作直線直線MN∥DE,若∠ACD=20°,試求∠CAM的大小.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖 AB=AC,CD⊥AB于D,BE⊥AC于E,BE與CD相交于點O.
(1)求證AD=AE;
(2)連接OA,BC,試判斷直線OA,BC的關系并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,A、B、C分別為數軸上的三點,A點對應的數為60,B點在A點的左側,并且與A點的距離為30,C點在B點左側,C點到A點距離是B點到A點距離的4倍.
![]()
(1)求出數軸上B點對應的數及AC的距離.
(2)點P從A點出發,以3單位/秒的速度向終點C運動,運動時間為t秒.
①當P點在AB之間運動時,則BP= .(用含t的代數式表示)
②P點自A點向C點運動過程中,何時P,A,B三點中其中一個點是另外兩個點的中點?求出相應的時間t.
③當P點運動到B點時,另一點Q以5單位/秒的速度從A點出發,也向C點運動,點Q到達C點后立即原速返回到A點,那么Q點在往返過程中與P點相遇幾次?直.接.寫.出.相遇時P點在數軸上對應的數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,P為AD邊上一點,沿直線BP將△ABP翻折至△EBP(點A的對應點為點E),PE與CD相交于點O,且OE=OD.
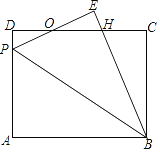
(1)求證:PE=DH;
(2)若AB=10,BC=8,求DP的長.
【答案】(1)見解析;(2)![]() .
.
【解析】試題分析:(1) 先證明△DOP≌△EOH,再利用等量代換得到PE=DH.
(2) 設DP=x, Rt△BCH中,先用 x表示三角形三邊,利用勾股定理列式解方程.
試題解析:
(1)解:證明:∵OD=OE,∠D=∠E=90°,∠DOP=∠EOH,
∴△DOP≌△EOH,
∴OP=OH,
∴PO+OE=OH+OD,
∴PE=DH.
(2)解:設DP=x,則EH=x,BH=10﹣x,
CH=CD﹣DH=CD﹣PE=10﹣(8﹣x)=2+x,
∴在Rt△BCH中,BC2+CH2=BH2
(2+x)2+82=(10﹣x)2,
∴x=![]() ,
,
∴DP=![]() .
.
【題型】解答題
【結束】
25
【題目】某文教店老板到批發市場選購A,B兩種品牌的繪圖工具套裝,每套A品牌套裝進價比B品牌每套套裝進價多2.5元,已知用200元購進A種套裝的數量是用75元購進B種套裝數量的2倍.
(1)求A,B兩種品牌套裝每套進價分別為多少元?
(2)若A品牌套裝每套售價為13元,B品牌套裝每套售價為9.5元,店老板決定,購進B品牌的數量比購進A品牌的數量的2倍還多4套,兩種工具套裝全部售出后,要使總的獲利超過120元,則最少購進A品牌工具套裝多少套?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 與
與![]() 在平面直角坐標系中的位置如圖所示.
在平面直角坐標系中的位置如圖所示.
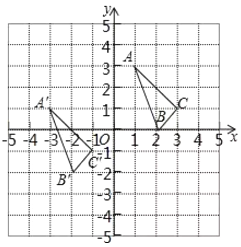
(1)分別寫出各點的坐標:![]() ___________,
___________,![]() _________,
_________,![]() _______________.
_______________.
(2)![]() 是由
是由![]() 經過怎樣的平移變換得到的?答:___________________.
經過怎樣的平移變換得到的?答:___________________.
(3)若點![]() 是
是![]() 內部一點,則
內部一點,則![]() 內部的對應點
內部的對應點![]() 的坐標為___________.
的坐標為___________.
(4)求![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com