【題目】點P，Q在數軸上分別表示的數分別為p，q，我們把p，q之差的絕對值叫做點P，Q之間的距離，即
．如圖，在數軸上，點A，B，O，C，D的位置如圖所示，則
；
；
．請探索下列問題：
（1）計算
____________，它表示哪兩個點之間的距離？________________________．
（2）點M為數軸上一點，它所表示的數為x，用含x的式子表示PB=____________；當PB=2時，x=____________；當x=____________時，|x+4|+|x-1|+|x-3|的值最小．
（3）|x-1|+|x-2|+|x-3|+…+|x-2018|+|x-2019|的最小值為________________________．
【答案】（1）5；A與C;（2）|x+2|；-4或0；1;（3）1019090
【解析】
（1）由所給信息，結合絕對值的性質可求；
（2）由絕對值的性質，分段去掉絕對值符號，在不同的x范圍內確定|x＋4|＋|x1|＋|x3|的最小值；
（3）由所給式子的對稱性，結合絕對值的性質，將所求絕對值式子轉化為求0＋2＋4＋…＋2018的和．
（1）|1（4）|＝|1＋4|＝|5|＝5，|1（4）|表示點A與C之間的距離，
故答案為：5，點A與C；
（2）∵點P為數軸上一點，它所表示的數為x，點B表示的數為2，
∴PB＝|x（2）|＝|x＋2|，
當PB＝2時，|x＋2|＝2，得x＝0或x＝4，
當x≤4時，|x＋4|＋|x1|＋|x3|＝x4＋1x＋3x＝x≥4；
當4＜x＜1時，|x＋4|＋|x1|＋|x3|＝x＋4＋1x＋3x＝8x，
當1≤x≤3時，|x＋4|＋|x1|＋|x3|＝x＋4＋x1＋3x＝6＋x，
當x＞3時，|x＋4|＋|x1|＋|x3|＝x＋4＋x1＋x3＝3x＞9，
∴當x＝1時，|x＋4|＋|x1|＋|x3|有最小值；
故答案為：|x＋2|；4或0；1
（3）|x1|＋|x2019|≥|12019|＝2018，
當且僅當1≤x≤2019時，|x1|＋|x2019|＝2018，
當且僅當2≤x≤2018時，|x2|＋|x2018|≥|22018|＝2016，
…
同理，當且僅當1009≤x≤1011時，|x1009|＋|x1011|≥|10091011|＝2，
|x1010|≥0，當x＝1010時，|x1010|＝0，
∴|x1|＋|x2|＋|x3|＋…＋|x2018|＋|x2019|≥0＋2＋4＋…＋2018＝1019090，
∴|x1|＋|x2|＋|x3|＋…＋|x2018|＋|x2019|的最小值為1019090；
故答案為1019090．
科目：初中數學 來源： 題型：
【題目】某縣教育局為了豐富初中學生的大課間活動，要求各學校開展形式多樣的陽光體育活動．某中學就“學生體育活動興趣愛好”的問題，隨機調查了本校某班的學生，并根據調查結果繪制成如下的不完整的扇形統計圖和條形統計圖：
（1）在這次調查中，喜歡籃球項目的同學有 人，在扇形統計圖中，“乒乓球”的百分比為 %，如果學校有800名學生，估計全校學生中有 人喜歡籃球項目．
（2）請將條形統計圖補充完整．
（3）在被調查的學生中，喜歡籃球的有2名女同學，其余為男同學．現要從中隨機抽取2名同學代表班級參加校籃球隊，請直接寫出所抽取的2名同學恰好是1名女同學和1名男同學的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有大小兩種貨車，
輛大貨車與
輛小火車一次可以運貨
噸，
輛大貨車與
輛小貨車一次可以運貨
噸.
（1）求
輛大貨車和輛小貨車一次可以分別運多少噸；
（2）現有
噸貨物需要運輸，貨運公司擬安排大小貨車共
輛把全部貨物一次運完.求至少需要安排幾輛大貨車？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】 某單位在二月份準備組織部分員工到北京旅游，現聯系了甲、乙兩家旅行社，兩家旅行社報價均為2000元/人，兩家旅行社同時都對10人以上的團體推出了優惠舉措：甲旅行社對每位員工七五折優惠；而乙旅行社是免去一位帶隊管理員工的費用，其余員工八折優惠．
(1)如果設參加旅游的員工共有a(a
)人，則甲旅行社的費用為 元，乙旅行社的費用為 元；(用含a的代數式表示，并化簡．)
(2)假如這個單位現組織包括管理員工在內的共20名員工到北京旅游，該單位選擇哪一家旅行社比較優惠？請說明理由；
(3)如果計劃在二月份外出旅游七天，設最中間一天的日期為m．
①這七天的日期之和為 ；(用含m的代數式表示，并化簡.)
②假如這七天的日期之和為63的倍數，則他們可能于二月幾號出發?(寫出所有符合條件的可能性，并寫出簡單的計算過程.)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某鄉鎮實施產業扶貧，幫助貧困戶承包了荒山種植蜜柚，已知該蜜柚的成本價為8元/千克。
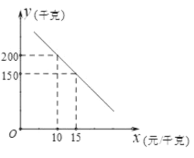
到了收獲季節，投入市場銷售時，調查市場行情，發現該蜜柚銷售不會虧本，且每天銷量
干克)與銷售單價x(元/千克)之間的函數關系如圖所示.
(1)求y與x的函數關系式，并寫出x的取值范圍:
(2)當該蜜柚定價為多少時，每天銷售獲得的利潤最大?最大利潤是多少?
(3)某農戶今年共采摘蜜柚4800千克，該蜜柚的保持期為40天，根據(2)中獲得最大利潤的方式進行銷售，能否銷售完這批蜜柚?請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
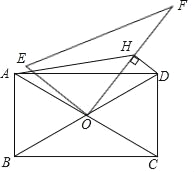
【題目】如圖，在矩形ABCD中，AB＝4，BC＝4
，對角線AC、BD相交于點O，現將一個直角三角板OEF的直角頂點與O重合，再繞著O點轉動三角板，并過點D作DH⊥OF于點H，連接AH．在轉動的過程中，AH的最小值為_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
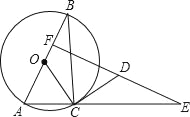
【題目】如圖，⊙O是Rt△ABC的外接圓，AB為直徑，∠ABC=30°，CD是⊙O的切線，ED⊥AB于F，
（1）求證：△CDE是等腰三角形；
（2）若AB=4，
，求證：△OBC≌△DCE．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知一次函數y=ax+b的圖象過點（﹣2，1），則關于拋物線y=ax2﹣bx+3的三條敘述：其中所有正確敘述的個數是（ ）
①過點（2，1），②對稱軸可以是x=1，③當a＜0時，其頂點的縱坐標的最小值為3．
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
