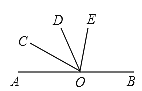
【題目】已知O為直線AB上一點，OC平分∠AOD，∠BOD=3∠DOE，∠COE=
則∠BOE的度數(shù)是
A. 
B. 
C. 
D. 
【答案】C
【解析】
設(shè)∠DOE=x，則∠BOD=3x，根據(jù)平角的定義可得∠AOD=180°-∠BOD=180°-3x；再根據(jù)角平分線的定義可得∠COD=
∠AOD=90°-
x．根據(jù)∠COE=∠COD+∠DOE可得方程90°-
=m，解方程求得x的值，即可求得∠BOE的度數(shù).
設(shè)∠DOE=x，則∠BOD=3x，
∴∠AOD=180°-∠BOD=180°-3x．
∵OC平分∠AOD，
∴∠COD=∠AOD=（180°-3x）=90°-x．
∵∠COE=∠COD+∠DOE=90°-x+x=90°- ，
由題意可得，90°-=m，解得x=180°-2m，即∠DOE=180°-2m，
∴∠BOE=360°-4m，
故選C．
高效智能課時作業(yè)系列答案
捷徑訓(xùn)練檢測卷系列答案科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，在四邊形ABCD中，AD∥BC，E為CD的中點，連接AE、BE，BE⊥AE，延長AE交BC的延長線于點F．求證：
（1）FC=AD；
（2）AB=BC+AD．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，點N是反比例函數(shù)y= 
（x＞0）圖象上的一個動點，過點N作MN∥x軸，交直線y=﹣2x+4于點M，則△OMN面積的最小值是（ ）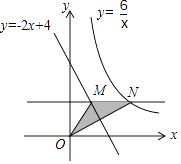
A.1
B.2
C.3
D.4
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】把下列各數(shù)填在相應(yīng)的大括號里：
－3，0.2，0，－|＋
|，－5%，－
，|－9|，－(－1)，－23，＋3
.
(1)正整數(shù)集合：{ …}；
(2)負(fù)分?jǐn)?shù)集合：{ …}；
(3)負(fù)數(shù)集合：{ …}；
(4)整數(shù)集合：{ …}；
(5)分?jǐn)?shù)集合：{ …}；
(6)非負(fù)數(shù)集合：{ …}．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】已知點
、
在
的
邊上，
，
，為了判斷
與
的大小關(guān)系，請你填空完成下面的推理過程，并在空白括號內(nèi)，注明推理的根據(jù)．
解：作
，垂足為
∵，
∴
是________三角形，
∴
________
又∵，
∴
________，即
________；
又∵________（自己所作），
∴
是線段________的垂直平分線；
∴
________
∴________．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
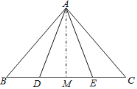
【題目】如圖，等腰三角形ABC的底邊BC長為4，面積是16，腰AC的垂直平分線EF分別交AC，AB邊于E，F點
若點D為BC邊的中點，點M為線段EF上一動點，則
周長的最小值為
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】下表中有兩種移動電話計費方式:
月使用費 | 主叫限定時間(分鐘) | 主叫超時費(元/分鐘) | 被叫 | |
方式一 | 65 | 160 | 0.20 | 免費 |
方式二 | 100 | 380 | 0.25 | 免費 |
(月使用費固定收；主叫不超過限定的時間不再收費,主叫超過限定時間的部分加收超時費；被叫免費)
(1)若張聰某月主叫通話時間為200分鐘,則他按方式一計費需____元,按方式二計費需____
元；李華某月按方式二計費需107元,則李華該月主叫通話時間為_____分鐘；
(2)是否存在某主叫通話時間
(分鐘),按方式一和方式二的計費相等?若存在,請求出的值；若不存在,請說明理由。
(3)直接寫出當(dāng)月主叫通話時間(分鐘)滿足什么條件時,選擇方式一省錢。
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】正方形A1B1C1O，A2B2C2C1 ， A3B3C3C2 ， …按如圖所示的方式放置．點A1 ， A2 ， A3 ， …和點C1 ， C2 ， C3 ， …分別在直線y=kx+b（k＞0）和x軸上，已知點B1（1，1），B2（3，2），則Bn的坐標(biāo)是 ．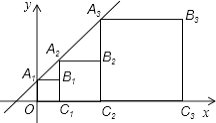 
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】已知：如圖，∠A+∠D=180°，∠1=3∠2，∠2=24°，點P是BC上的一點.
（1）請寫出圖中∠1的一對同位角，一對內(nèi)錯角，一對同旁內(nèi)角；
（2）求∠EFC與∠E的度數(shù)；
（3）若∠BFP=46°，請判斷CE與PF是否平行？
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com