
【題目】如圖,在正方形ABCD中,以AB為邊在正方形內作等邊△ABE,連接DE,CE,則∠CED的度數為 . 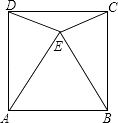
【答案】150°
【解析】解:∵四邊形ABCD是正方形,
∴∠BAD=∠ABC=∠ADC=∠BCD=90°,AB=BC=CD=DA,
∵△ABE是等邊三角形,
∴AB=AE=BE,∠BAE=∠ABE=60°,
∴AE=AD=BE=BC,∠DAE=∠CBE=30°,
∴∠ADE=∠BCE= ![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∴∠EDC=∠ECD=15°,
∴∠CED=180°﹣15°﹣15°=150°.
所以答案是:150°.
【考點精析】本題主要考查了等邊三角形的性質和正方形的性質的相關知識點,需要掌握等邊三角形的三個角都相等并且每個角都是60°;正方形四個角都是直角,四條邊都相等;正方形的兩條對角線相等,并且互相垂直平分,每條對角線平分一組對角;正方形的一條對角線把正方形分成兩個全等的等腰直角三角形;正方形的對角線與邊的夾角是45o;正方形的兩條對角線把這個正方形分成四個全等的等腰直角三角形才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,點E是BC的中點,將△ABE沿AE折疊后得到△AFE,點F在正方形ABCD的內部,延長AF交CD于點G.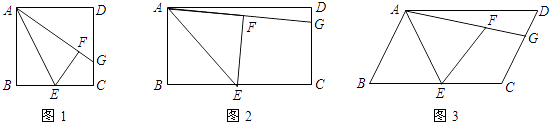
(1)猜想并證明線段GF與GC的數量關系;
(2)若將圖1中的正方形改成矩形,其它條件不變,如圖2,那么線段GF與GC之間的數量關系是否改變?請證明你的結論;
(3)若將圖1中的正方形改成平行四邊形,其它條件不變,如圖3,那么線段GF與GC之間的數量關系是否會改變?請證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是一個圓,一只電子跳蚤在標有五個數字的點上跳躍,若它停在奇數點上,則下一次沿順時針方向跳兩個點;若停在偶數點上,則下一次沿逆時針方向跳一個點,若跳蚤從2這點開始跳,則經2017次跳后它停在數____對應的點上.
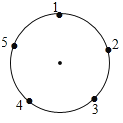
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,過點C的直線MN∥AB,D為AB邊上一點,過點D作DE⊥BC,交直線MN于E,垂足為F,連接CD、BE. 
(1)求證:CE=AD;
(2)當D在AB中點時,四邊形BECD是什么特殊四邊形?說明你的理由;
(3)若D為AB中點,則當∠A的大小滿足什么條件時,四邊形BECD是正方形?請說明你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校規定:學生的數學學期綜合成績是由平時、期中和期末三項成績按3:3:4的比例計算所得.若某同學本學期數學的平時、期中和期末成績分別是90分,90分和85分,則他本學期數學學期綜合成績是分.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com