
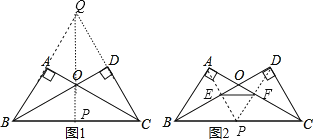
【題目】如圖,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC與BD相交于點O,限用無刻度直尺完成以下作圖:
(1)在圖1中作線段BC的中點P;
(2)在圖2中,在OB、OC上分別取點E、F,使EF∥BC.

【答案】(1)見解析;(2)見解析.
【解析】
(1)延長BA和CD,它們相交于點Q,然后延長QO交BC于P,則PB=PC,根據線段垂直平分線的逆定理可證明;
(2)連結AP交OB于E,連結DP交OC于F,則EF∥BC.分別證明△BEP≌△CFP,△BEP≌△CFP可得∠APB=∠DPC和∠PEF=∠PFE,根據三角形內角和定理和平角的定義可得∠APB=∠PEF,即可證明EF//BC.
解:(1)如圖1,點P為所作,
理由如下:∵∠A=∠D=90°,AC=BD,BC=CB,
∴△ABC≌△DCB
∴∠ABC=∠DCB,∠ACB=∠DBC
∴QB=QC,OB=OC
∴Q,O在BC的垂直平分線上,
∴延長QO交BC于P,就有P為線段BC的中點;
(2)如圖2,EF為所作.
理由如下:∵△ABC≌△DCB
∴AB=DC,
又∵∠ABC=∠DCB,BP=PC
∴△ABP≌△DCP
∴∠APB=∠DPC
又∵∠DBC=∠ACB,BP=PC
∴△BEP≌△CFP
∴PE=PF
∴∠PEF=∠PFE,
∵∠APB+∠DPC+∠APD=180°
∠PEF+∠PFE+∠APD=180°
∴∠APB=∠PEF
∴EF//BC.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
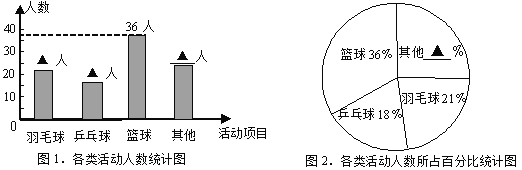
【題目】學校為統籌安排大課間體育活動,在各班隨機選取了一部分學生,分成四類活動:“籃球”、 “羽毛球”、 “乒乓球”、“其他”進行調查,整理收集到的數據,繪制成如下的兩幅統計圖.
(1)學校采用的調查方式是 ;學校共隨機選取了 名學生;
(2)補全統計圖中的數據:羽毛球 人、乒乓球 人、其他 人、其他 ﹪;
(3)該校共有1100名學生,請估計喜歡“籃球”的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“知識改變命運,科技繁榮祖國”.我市中小學每年都要舉辦一屆科技運動會.下圖為我市某校2009年參加科技運動會航模比賽(包括空模、海模、車模、建模四個類別)的參賽人數統計圖:
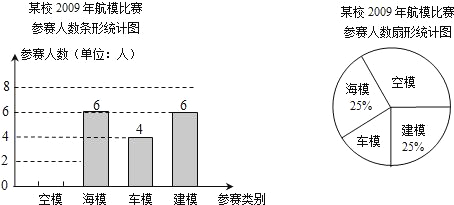
(1)該校參加車模、建模比賽的人數分別是 人和 人;
(2)該校參加航模比賽的總人數是 人,空模所在扇形的圓心角的度數是 °,并把條形統計圖補充完整;(溫馨提示:作圖時別忘了用0.5毫米及以上的黑色簽字筆涂黑)
(3)從全市中小學參加航模比賽選手中隨機抽取80人,其中有32人獲獎.今年我市中小學參加航模比賽人數共有2485人,請你估算今年參加航模比賽的獲獎人數約是多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖1所示是一枚質地均勻的骰子.骰子有六個面并分別代表數字1,2,3,4,5,6.如圖2,正六邊形ABCDEF的頂點處各有一個圈.跳圈游戲的規則為:游戲者每擲一次骰子,骰子向上的一面上的點數是幾,就沿正六邊形的邊順時針方向連續跳幾個邊長.如:若從圈A起跳,第一次擲得3,就順時針連續跳3個邊長,落到圈D;若第二次擲得2,就從圈D開始順時針連續跳2個邊長,落到圈F……
設游戲者從圈A起跳.
(1)小明隨機擲一次骰子,求落回到圈A的概率P1;
(2)小亮隨機擲兩次骰子,用列表法或畫樹狀圖法求最后落回到圈A的概率P2,并指出他與小明落回到圈A的可能性一樣嗎?
 圖1
圖1 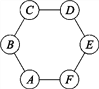 圖2
圖2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知數軸上有A、B、C三點,點A和點B間距20個單位長度且點A、B表示的有理數互為相反數,AC=36,數軸上有一動點P從點A出發,以每秒1個單位長度的速度沿數軸向終點C移動,設移動時間為t秒.
![]()
(1)點A表示的有理數是 ,點B表示的有理數是 ,點C表示的有理數是 .
(2)當點P運動到點B時,點Q從點O出發,以每秒6個單位長度的速度沿數軸在點O和點C之間往復運動.
①求t為何值時,點Q第一次與點P重合?
②當點P運動到點C時,點Q的運動停止,求此時點Q一共運動了多少個單位長度,并求出此時點Q在數軸上所表示的有理數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學決定在本校學生中開展足球、籃球、羽毛球、乒乓球四種活動,為了了解學生對這四種活動的喜愛情況,學校隨機調查了該校m名學生,看他們喜愛哪一種活動(每名學生必選一種且只能從這四種活動中選擇一種),現將調查的結果繪制成如下不完整的統計圖.請你根據圖中的信息,解答下列問題.

(1)m= ,n= ;
(2)請補全圖中的條形圖;
(3)扇形統計圖中,足球部分的圓心角是 度;
(4)根據抽樣調查的結果,請估算全校1800名學生中,大約有多少人喜愛踢足球.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解決問題,一輛貨車從超市出發,向東走了3千米到達小彬家,繼續走2.5千米到達小穎家,然后向西走了10千米到達小明家,最后回到超市.
(1)以超市為原點,以向東的方向為正方向,用1個單位長度表示1千米,在數軸上表示出小明家.
(2)小明家距小彬家多遠?
(3)貨車一共行駛的多少千米?
(4)貨車每千米耗油0.2升,這次共耗油多少升?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題:①有兩個角和第三個角的平分線對應相等的兩個三角形全等;②有兩條邊和第三條邊上的中線對應相等的兩個三角形全等;③有兩條邊和第三條邊上的高對應相等的兩個三角形全等.其中正確的是( )
A. ①② B. ②③ C. ①③ D. ①②③
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com