
【題目】如圖,從地面上的點A看一山坡上的電線桿PQ,測得桿頂端點P的仰角是45°,向前走6m到達B點,測得桿頂端點P和桿底端點Q的仰角分別是60°和30°.
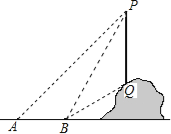
(1)求∠BPQ的度數;
(2)求該電線桿PQ的高度(結果精確到1m).
備用數據:![]() ,
,![]() .
.
【答案】(1)30°;(2)9m.
【解析】試題分析:(1)延長PQ交直線AB于點E,根據直角三角形兩銳角互余求得即可;
(2)設PE=x米,在直角△APE和直角△BPE中,根據三角函數利用x表示出AE和BE,根據AB=AE-BE即可列出方程求得x的值,再在直角△BQE中利用三角函數求得QE的長,則PQ的長度即可求解.
試題解析:延長PQ交直線AB于點E,
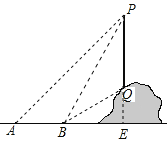
(1)∠BPQ=90°-60°=30°;
(2)設PE=x米.
在直角△APE中,∠A=45°,
則AE=PE=x米;
∵∠PBE=60°
∴∠BPE=30°
在直角△BPE中,BE=![]() PE=
PE=![]() x米,
x米,
∵AB=AE-BE=6米,
則x-![]() x=6,
x=6,
解得:x=9+3![]() .
.
則BE=(3![]() +3)米.
+3)米.
在直角△BEQ中,QE=![]() BE=
BE=![]() (3
(3![]() +3)=(3+
+3)=(3+![]() )米.
)米.
∴PQ=PE-QE=9+3![]() -(3+
-(3+![]() )=6+2
)=6+2![]() ≈9(米).
≈9(米).
答:電線桿PQ的高度約9米.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:初中數學 來源: 題型:
【題目】已知拋物線![]() 經過A(3,0)、B(4,1)兩點,且與y軸交于點C.
經過A(3,0)、B(4,1)兩點,且與y軸交于點C.
(1)求拋物線的解析式;
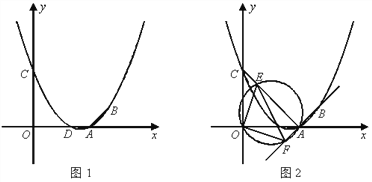
(2)如圖1,設拋物線與x軸的另一個交點為D,在拋物線的對稱軸上找一點H,使△CDH的周長最小,求出H點的坐標并求出最小周長值;
(3)如圖2,連接AC,E為線段AC上任意一點(不與A、C重合),經過A、E、O三點的圓交直線AB于點F,當△OEF的面積取得最小值時,求面積的最小值及E點坐標。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩個倉庫共存有糧食60![]() .解決下列問題,3個小題都要寫出必要的解題過程:
.解決下列問題,3個小題都要寫出必要的解題過程:
(1)甲倉庫運進糧食14![]() ,乙倉庫運出糧食10
,乙倉庫運出糧食10![]() 后,兩個倉庫的糧食數量相等.甲、乙兩個倉庫原來各有多少糧食?
后,兩個倉庫的糧食數量相等.甲、乙兩個倉庫原來各有多少糧食?
(2)如果甲倉庫原有的糧食比乙倉庫的2倍少3![]() ,則甲倉庫運出多少
,則甲倉庫運出多少![]() 糧食給乙倉庫,可使甲、乙兩倉庫糧食數量相等?
糧食給乙倉庫,可使甲、乙兩倉庫糧食數量相等?
(3)甲乙兩倉庫同時運進糧食,甲倉庫運進的數量比本倉庫原存糧食數量的一半多1![]() ,乙倉庫運進的數量是本倉庫原有糧食數量加上8
,乙倉庫運進的數量是本倉庫原有糧食數量加上8![]() 所得的和的一半.求此時甲、乙兩倉庫共有糧食多少
所得的和的一半.求此時甲、乙兩倉庫共有糧食多少![]() ?
?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD的對角線AC,BD相交于點O,點E,F分別是線段AO,BO的中點,若AC+BD=24厘米,△OAB的周長是18厘米,則EF為( ) 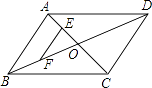
A.3厘米
B.4厘米
C.5厘米
D.6厘米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在①ab是一次單項式;②單項式﹣x2y的系數是﹣1;③3+x2﹣4x是按x的降冪排列的;④數4是單項式;這四句話中不正確的是( )
A.①③
B.②③
C.②④
D.①②
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將代數式3x2y+5xy2﹣3y3﹣5x3按y的降冪排列是( )
A.﹣5x3+3x2y+5xy2﹣3y3
B.﹣3y3+5xy2+3x2y﹣5x3
C.﹣5x3﹣3y3+3x2y+5xy2
D.3x2y+5xy2﹣3y3﹣5x3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,設正方體ABCD﹣A1B1C1D1的棱長為1,黑、白兩個甲殼蟲同時從點A出發,以相同的速度分別沿棱向前爬行,黑甲殼蟲爬行的路線是AA1→A1D1→…,白甲殼蟲爬行的路線是AB→BB1→…,并且都遵循如下規則:所爬行的第n+2與第n條棱所在的直線必須是既不平行也不相交(其中n是正整數).那么當黑、白兩個甲殼蟲各爬行完第2013條棱分別停止在所到的正方體頂點處時,它們之間的距離是( ) 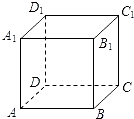
A.0
B.1
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com