
【題目】如圖,反比例函數y=![]() (k<0)的圖象與矩形ABCD的邊相交于E、F兩點,且BE=2AE,E(﹣1,2).
(k<0)的圖象與矩形ABCD的邊相交于E、F兩點,且BE=2AE,E(﹣1,2).

(1)求反比例函數的解析式;
(2)連接EF,求△BEF的面積.
【答案】(1)y=![]() (2)
(2)![]()
【解析】
試題分析:(1)將E(﹣1,2)代入y=![]() ,利用待定系數法即可求出反比例函數的解析式;
,利用待定系數法即可求出反比例函數的解析式;
(2)由矩形的性質及已知條件可得B(﹣3,2),再將x=﹣3代入y=﹣![]() ,求出y的值,得到CF=
,求出y的值,得到CF=![]() ,那么BF=2﹣
,那么BF=2﹣![]() =
=![]() ,然后根據△BEF的面積=
,然后根據△BEF的面積=![]() BEBF,將數值代入計算即可.
BEBF,將數值代入計算即可.
試題解析:(1)∵反比例函數y=![]() (k<0)的圖象過點E(﹣1,2),
(k<0)的圖象過點E(﹣1,2),
∴k=﹣1×2=﹣2,
∴反比例函數的解析式為y=﹣![]() ;
;
(2)∵E(﹣1,2),
∴AE=1,OA=2,
∴BE=2AE=2,
∴AB=AE+BE=1+2=3,
∴B(﹣3,2).
將x=﹣3代入y=﹣![]() ,得y=
,得y=![]() ,
,
∴CF=![]() ,
,
∴BF=2﹣![]() =
=![]() ,
,
∴△BEF的面積=![]() BEBF=
BEBF=![]() ×2×
×2×![]() =
=![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
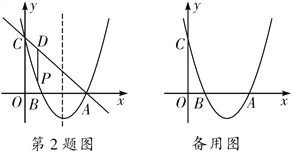
【題目】如圖,拋物線y=x2+bx+c過點A(3,0),B(1,0),交y軸于點C,點P是該拋物線上一動點,點P從C點沿拋物線向A點運動(點P不與點A重合),過點P作PD∥y軸交直線AC于點D.
(1)求拋物線的解析式;
(2)求點P在運動的過程中線段PD長度的最大值;
(3)在拋物線對稱軸上是否存在點M,使|MA-MC|最大?若存在,請求出點M的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年某市約有108000名應屆初中畢業生參加中考,按四舍五入保留兩位有效數字,108000用科學計數法表示為( )
(A)0.10×106 (B)1.08×105 (C)0.11×106 (D)1.1×105
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=2,∠BAC=20°.動點P、Q分別在直線BC上運動,且始終保持∠PAQ=100°.設BP=x,CQ=y,則y與x之間的函數關系用圖象大致可以表示為( )

A. 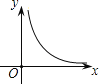 B.
B. 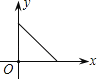 C.
C.  D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=-(x+k)2+h,當x>-2時,y隨x的增大而減小,則函數中k的取值范圍是( )
A. k≥-2 B. k≤-2 C. k≥2 D. k≤2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com