
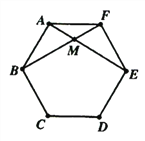
【題目】如圖,正六邊形ABCDEF的對角線AE與BF相交于點M.
(1)求證:△ABM≌△FEM;
(2)已知AM=2,求BF的長度.
【答案】(1)證明見解析;(2)6
【解析】試題分析:(1)由ASA定理證明△ABM≌△DEN即可;
(2)由30°角所對直角邊等于斜邊的一半,得到BM的長,再由全等三角形的性質得到AM的長,從而求出BF的長.
試題解析:解:(1)∵六邊形ABCDEF是正六邊形,∴AB=DE,∠BAF=120°,∴∠ABM=30°,∴∠BAM=90°,同理∠AEF=30°,∠EFM=90°,∴∠ABM=∠AEF,∠BAM=∠EFM,在△ABM和△DEN中, 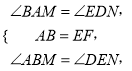
∴△ABM≌△DEN(ASA).
(2)∵在Rt△ABM中,∠ABM=30°,∴BM=2AM=4.
∵△ABM≌△DEN,∴AM=2,∴BF=BM+FM=4+2=6.


科目:初中數學 來源: 題型:
【題目】計算:
(1)﹣8﹣4+6
(2)(﹣52)﹣(+8)﹣(﹣4)
(3)﹣8×(﹣15)
(4)(﹣ ![]() )÷(﹣
)÷(﹣ ![]() )
)
(5)﹣ ![]()
(6)﹣3×(﹣ ![]() )3 .
)3 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在50包型號為L的襯衫的包裹中混進了型號為M的襯衫,每包20件襯衫,每包中混入的M號襯衫數如表:
M號襯衫數 | 0 | 1 | 4 | 5 | 7 | 9 | 10 | 11 |
包數 | 7 | 3 | 10 | 15 | 5 | 4 | 3 | 3 |
根據以上數據,選擇正確選項( ).
A.M號襯衫一共有47件
B.從中隨機取一包,包中L號襯衫數不低于9是隨機事件
C.從中隨機取一包,包中L號襯衫數不超過4的概率為0.26
D.將50包襯衫混合在一起,從中隨機拿出一件襯衫,恰好是M號的概率為0.252
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把下列各數填入表示它所在的數集的大括號:
﹣2.4,3,21.08,0,﹣100,﹣(﹣2.28),﹣ ![]() ,﹣|﹣4|,
,﹣|﹣4|,
正有理數集合:{}
負有理數集合:{}
整數集合:{}
分數集合:{}.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com