Question

【題目】將兩塊大小一樣含30°角的直角三角板，疊放在一起，使得它們的斜邊AB重合，直角邊不重合，已知AB=8，BC=AD=4，AC與BD相交于點E，連接CD．

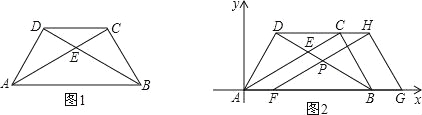
（1）填空：如圖1，AC的長度= ，tan∠ABD= ；

（2）試判斷△ADC與△AEB的關系，并說明理由；

（3）如圖2建立平面直角坐標系，保持△ABD不動，將△ABC向x軸的正方向平移到△FGH的位置，FH與BD相交于點P，設AF=t，△FBP面積為S，求S與t之間的函數關系式，并寫出t的取值范圍．

Answer 1

【答案】（1）4，；（2）△ADC∽△AEB，理由見解析；（3）S=（8﹣t）2，t的取值范圍為：0≤t＜8

【解析】

試題分析：（1）首先根據題意得：DC∥AB，∠ADB=∠ACB=90°，∠ABD=∠CAB=30°，然后由勾股定理，求得AC與BD的長，（2）根據兩個含30°的直角三角板直接求出∠DAC=∠EAB=30°，∠AEB=∠ADC=120，即可得出△ADC∽△AEB．（3）過P作出△FBP的高．△FBP面積應等于FB×PK÷2，易得FB=AB﹣AF=8﹣t；則KB等于FB的一半，利用30°的正切值可求得FK的值．

試題解析：（1）根據題意得：DC∥AB，∠ADB=∠ACB=90°，∠ABD=∠CAB=30°，

∵AB=8，BC=AD=4，

∴AC=BD=4，∠ABD=30°，

∴tan∠ABD=tan30°=，

（2）△ADC∽△AEB，

理由：∵∠BAD=∠ABC=60°，∠BAC=∠ABD=30°，

∴∠DAC=∠CBD=∠BAC=30°，AE=BE，

∴∠AEB=180°﹣∠EAB﹣∠EBA=120°，

∵AC=BD，

∴ED=EC，

∴∠BDC=∠ACD=（180°﹣∠DEC）=30°，

∵∠ADB=90°

∴∠ADC=∠ADB+∠BDC=120°=∠AEB，

∵∠DAC=∠BAC，

∴△ADC∽△AEB，

（3）（3）由題意知，FP∥AE，

∴∠1=∠PFB，

又∵∠1=∠2=30°，

∴∠PFB=∠2=30°，

∴FP=BP

過點P作PK⊥FB于點K，則FK=BK=FB．

∵AF=t，AB=8，

∴FB=8﹣t，BK=（8﹣t）．

在Rt△BPK中，PK=BKtan∠2=（8﹣t）tan30°=（8﹣t）．

∴△FBP的面積S=FBPK=（8﹣t）（8﹣t），

∴S與t之間的函數關系式為：

S=（8﹣t）2，

t的取值范圍為：0≤t＜8