
【題目】已知拋物線y= ![]() x2+1具有如下性質(zhì):該拋物線上任意一點到定點F(0,2)的距離與到x軸的距離始終相等,如圖,點M的坐標(biāo)為(
x2+1具有如下性質(zhì):該拋物線上任意一點到定點F(0,2)的距離與到x軸的距離始終相等,如圖,點M的坐標(biāo)為( ![]() ,3),P是拋物線y=
,3),P是拋物線y= ![]() x2+1上一個動點,則△PMF周長的最小值是( )
x2+1上一個動點,則△PMF周長的最小值是( ) 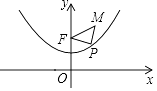
A.3
B.4
C.5
D.6
【答案】C
【解析】解:過點M作ME⊥x軸于點E,交拋物線y= ![]() x2+1于點P,此時△PMF周長最小值, ∵F(0,2)、M(
x2+1于點P,此時△PMF周長最小值, ∵F(0,2)、M( ![]() ,3),
,3),
∴ME=3,F(xiàn)M= ![]() =2,
=2,
∴△PMF周長的最小值=ME+FM=3+2=5.
故選C.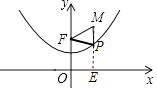
【考點精析】關(guān)于本題考查的二次函數(shù)的性質(zhì)和三角形三邊關(guān)系,需要了解增減性:當(dāng)a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當(dāng)a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小;三角形兩邊之和大于第三邊;三角形兩邊之差小于第三邊;不符合定理的三條線段,不能組成三角形的三邊才能得出正確答案.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】某廠去年的總產(chǎn)值比總支出多500萬元,而今年計劃的總產(chǎn)值比總支出多950萬元.已知今年計劃總產(chǎn)值比去年增加15%,而今年計劃總支出比去年減少10%.求今年計劃的總產(chǎn)值和總支出各為多少.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知△ABC在平面直角坐標(biāo)系中的位置如圖所示,直線l過點M(3,0)且平行于y軸.
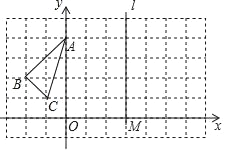
(1)作出△ABC關(guān)于y軸對稱的△A1B1C1,并寫出△A1B1C1各頂點的坐標(biāo).
(2)如果點P的坐標(biāo)是(﹣a,0),其中a>0,點P關(guān)于y軸的對稱點是P1,點P1關(guān)于直線l的對稱點是P2,求P1P2的長.(用含a的代數(shù)式表示)
(3)通過計算加以判斷,PP2的長會不會隨點P位置的變化而變化.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,△ABC中,∠ACB=90°,AC=BC,點E是AC上一點,連接BE. 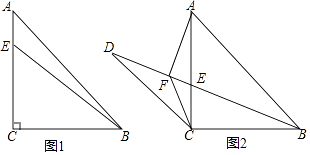
(1)如圖1,若AB=4 ![]() ,BE=5,求AE的長;
,BE=5,求AE的長;
(2)如圖2,點D是線段BE延長線上一點,過點A作AF⊥BD于點F,連接CD、CF,當(dāng)AF=DF時,求證:DC=BC.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,拋物線y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() 與x軸交于A、B兩點(點A在點B的左側(cè)),與y軸交于點C,對稱軸與x軸交于點D,點E(4,n)在拋物線上.
與x軸交于A、B兩點(點A在點B的左側(cè)),與y軸交于點C,對稱軸與x軸交于點D,點E(4,n)在拋物線上.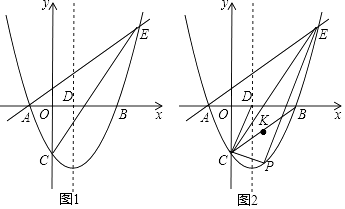
(1)求直線AE的解析式;
(2)點P為直線CE下方拋物線上的一點,連接PC,PE.當(dāng)△PCE的面積最大時,連接CD,CB,點K是線段CB的中點,點M是CP上的一點,點N是CD上的一點,求KM+MN+NK的最小值;
(3)點G是線段CE的中點,將拋物線y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() 沿x軸正方向平移得到新拋物線y′,y′經(jīng)過點D,y′的頂點為點F.在新拋物線y′的對稱軸上,是否存在一點Q,使得△FGQ為等腰三角形?若存在,直接寫出點Q的坐標(biāo);若不存在,請說明理由.
沿x軸正方向平移得到新拋物線y′,y′經(jīng)過點D,y′的頂點為點F.在新拋物線y′的對稱軸上,是否存在一點Q,使得△FGQ為等腰三角形?若存在,直接寫出點Q的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某中學(xué)為打造書香校園,計劃購進甲、乙兩種規(guī)格的書柜放置新購進的圖書,調(diào)查發(fā)現(xiàn),若購買甲種書柜3個、乙種書柜2個,共需資金1020元;若購買甲種書柜4個,乙種書柜3個,共需資金1440元.
(1)甲、乙兩種書柜每個的價格分別是多少元?
(2)若該校計劃購進這兩種規(guī)格的書柜共20個,其中乙種書柜的數(shù)量不少于甲種書柜的數(shù)量,學(xué)校至多能夠提供資金4320元,請設(shè)計幾種購買方案供這個學(xué)校選擇.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】一次函數(shù)y=kx+b(k≠0)的圖象經(jīng)過點A(2,﹣6),且與反比例函數(shù)y=﹣ ![]() 的圖象交于點B(a,4)
的圖象交于點B(a,4)
(1)求一次函數(shù)的解析式;
(2)將直線AB向上平移10個單位后得到直線l:y1=k1x+b1(k1≠0),l與反比例函數(shù)y2= ![]() 的圖象相交,求使y1<y2成立的x的取值范圍.
的圖象相交,求使y1<y2成立的x的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,反比例函數(shù)y= ![]() (x>0)的圖象與邊長是6的正方形OABC的兩邊AB,BC分別相交于M,N 兩點,△OMN的面積為10.若動點P在x軸上,則PM+PN的最小值是( )
(x>0)的圖象與邊長是6的正方形OABC的兩邊AB,BC分別相交于M,N 兩點,△OMN的面積為10.若動點P在x軸上,則PM+PN的最小值是( )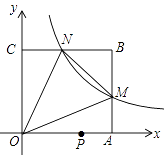
A.6 ![]()
B.10
C.2 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】將一幅三角板拼成如圖所示的圖形,過點C作CF平分∠DCE交DE于點F.

(1)求證:CF∥AB.
(2)求∠DFC的度數(shù).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com