
【題目】如圖,在平面直角坐標系 ![]() 中,定義直線
中,定義直線 ![]() 與雙曲線
與雙曲線 ![]() 的交點
的交點 ![]() (m、n為正整數)為 “雙曲格點”,雙曲線
(m、n為正整數)為 “雙曲格點”,雙曲線 ![]() 在第一象限內的部分沿著豎直方向平移或以平行于
在第一象限內的部分沿著豎直方向平移或以平行于 ![]() 軸的直線為對稱軸進行翻折之后得到的函數圖象為其“派生曲線”.
軸的直線為對稱軸進行翻折之后得到的函數圖象為其“派生曲線”.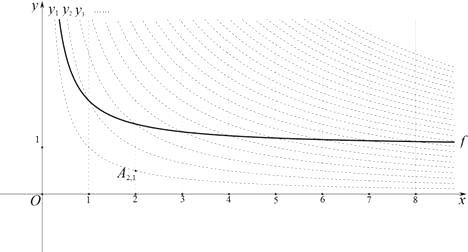
(1)①“雙曲格點” ![]() 的坐標為;
的坐標為;
②若線段 ![]() 的長為1個單位長度,則n=;
的長為1個單位長度,則n=;
(2)圖中的曲線 ![]() 是雙曲線
是雙曲線 ![]() 的一條“派生曲線”,且經過點
的一條“派生曲線”,且經過點 ![]() ,則
,則 ![]() 的解析式為 y=;
的解析式為 y=;
(3)畫出雙曲線 ![]() 的“派生曲線”g(g與雙曲線
的“派生曲線”g(g與雙曲線 ![]() 不重合),使其經過“雙曲格點”
不重合),使其經過“雙曲格點” ![]() 、
、 ![]() 、
、 ![]() .
.
【答案】
(1)(2,![]() ),7
),7
(2)![]()
(3)解:如圖:
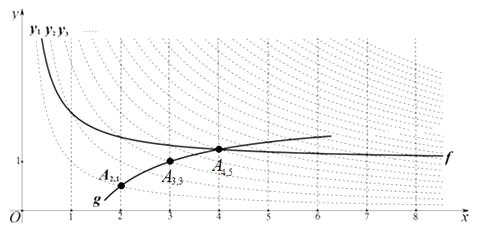
【解析】解:(1)①把x=2代入y= ![]() 得:y=
得:y= ![]() ,
,
則A的坐標是(2, ![]() );
);
②把x=4代入y= ![]() 得y=
得y= ![]() .
.
根據題意得:(4-2)2+( ![]() -
- ![]() )2=1,
)2=1,
解得:n=7.
所以答案是: (2, ![]() ),7;
),7;
( 2 )把x=2代入y= ![]() 得y=
得y= ![]() ,則點A2,3的坐標是(2,
,則點A2,3的坐標是(2, ![]() )。
)。
設f的解析式為y= ![]() +k,
+k,
把(2, ![]() )代入,得
)代入,得 ![]() ,
,
解得:k=1.
則f的解析式是:y= ![]() +1;
+1;
( 3 )把x=2代入y= ![]() 得y=
得y= ![]() ,則,A2,a的坐標是(2,
,則,A2,a的坐標是(2, ![]() );
);
把x=3代入y= ![]() 得y=1,則A3,3的坐標是(3,1);
得y=1,則A3,3的坐標是(3,1);
把x=4代入y= ![]() 得y=
得y= ![]() ,則A4,b的坐標是(4,
,則A4,b的坐標是(4, ![]() );
);
如圖:
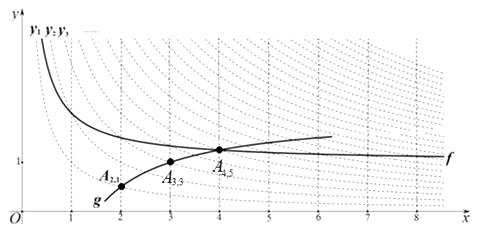
【考點精析】解答此題的關鍵在于理解比例系數k的幾何意義的相關知識,掌握幾何意義:表示反比例函數圖像上的點向兩坐標軸所作的垂線段與兩坐標軸圍成的矩形的面積.


科目:初中數學 來源: 題型:
【題目】某超市準備購進甲、乙兩種品牌的文具盒,甲、乙兩種玩具盒的進價和售價如下表,預計購進乙品牌文具盒的數量y(個)與甲品牌玩具盒數量x(個)之間的函數關系如圖所示.
甲 | 乙 | |
進價(元) | 15 | 30 |
售價(元) | 20 | 38 |
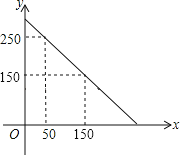
(1)y與x之間的函數關系式是 ;
(2)若超市準備用不超過6000元購進甲、乙兩種文具盒,則至少購進多少個甲種文具盒?
(3)在(2)的條件下,寫出銷售所得的利潤W(元)與x(個)之間的關系式,并求出獲得的最大利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AB⊥BC,AD∥BC,∠BCD=120°,BC=2,AD=DC.P為四邊形ABCD邊上的任意一點,當∠BPC=30°時,CP的長為 . 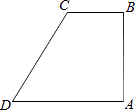
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將一個等腰直角三角形按圖示方式依次翻折,則下列說法正確的個數有( )

①DF平分∠BDE;②△BFD是等腰三角形;;③△CED的周長等于BC的長.
A. 0個; B. 1個; C. 2個; D. 3個.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系 ![]() 中,雙曲線
中,雙曲線 ![]() 與直線
與直線 ![]() 交于點A(3,1).
交于點A(3,1).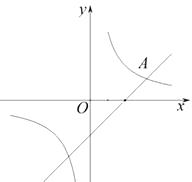
(1)求直線和雙曲線的解析式;
(2)直線 ![]() 與x軸交于點B,點P是雙曲線
與x軸交于點B,點P是雙曲線 ![]() 上一點,過點P作直線PC∥x軸,交y軸于點C,交直線
上一點,過點P作直線PC∥x軸,交y軸于點C,交直線 ![]() 于點D.若DC=2OB,直接寫出點
于點D.若DC=2OB,直接寫出點 ![]() 的坐標為 .
的坐標為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AD∥BC,∠ABC=∠ADC=90°,對角線AC,BD交于點O,DE平分∠ADC交BC于點E,連接OE.
(1)求證:四邊形ABCD是矩形;
(2)若AB=2,求△OEC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合題
(1)如圖1,△ABC中, ![]() ,AB的垂直平分線交AC于點D,連接BD.若AC=2,BC=1,則△BCD的周長為;
,AB的垂直平分線交AC于點D,連接BD.若AC=2,BC=1,則△BCD的周長為;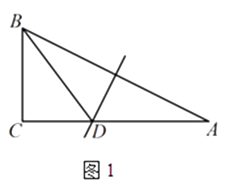
(2)O為正方形ABCD的中心,E為CD邊上一點,F為AD邊上一點,且△EDF的周長等于AD的長.
①在圖2中求作△EDF(要求:尺規作圖,不寫作法,保留作圖痕跡);
②在圖3中補全圖形,求 ![]() 的度數;
的度數;
③若 ![]() ,則
,則 ![]() 的值為 .
的值為 . 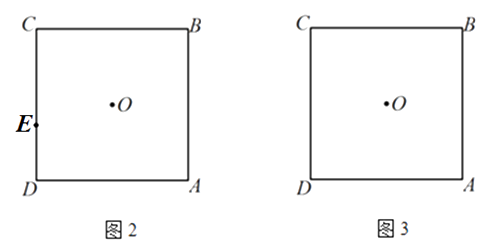
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC為銳角,點D為直線BC上一動點,以AD為直角邊且在AD的右側作等腰直角三角形ADE,∠DAE=90°,AD=AE.
(1)如果AB=AC,∠BAC=90°.①當點D在線段BC上時,如圖1,線段CE、BD的位置關系為___________,數量關系為___________
②當點D在線段BC的延長線上時,如圖2,①中的結論是否仍然成立,請說明理由.
(2)如圖3,如果AB≠AC,∠BAC≠90°,點D在線段BC上運動。探究:當∠ACB多少度時,CE⊥BC?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() 和點
和點![]() 在數軸上對應的數分別為
在數軸上對應的數分別為![]() 和
和![]() ,且
,且![]() .
.
![]()
(1)求線段![]() 的長;
的長;
(2)點![]() 在數軸上所對應的數為
在數軸上所對應的數為![]() ,且
,且![]() 是方程
是方程![]() 的解,點
的解,點![]() 在線段
在線段![]() 上,并且
上,并且![]()
![]() ,請求出點
,請求出點![]() 在數軸上所對應的數;
在數軸上所對應的數;
(3)在(2)的條件下,線段![]() 和
和![]() 分別以
分別以![]() 個單位長度/秒和
個單位長度/秒和![]() 個單位長度/秒的速度同時向右運動,運動時間為
個單位長度/秒的速度同時向右運動,運動時間為![]() 秒,
秒,![]() 為線段
為線段![]() 的中點,
的中點,![]() 為線段
為線段![]() 的中點,若
的中點,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com