
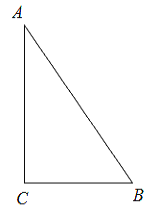
【題目】如圖,△ABC中,∠C=90°,AB=5cm,BC=3cm,若動點P從點C開始,按C→A→B→C的路徑運動,且速度為每秒1cm,設出發的時間為t秒.
(1)出發2秒后,求△ABP的周長;
(2)問t滿足什么條件時,△BCP為直角三角形;
(3)另有一點Q,從點C開始,按C→B→A→C的路徑運動,且速度為每秒2cm,若P、Q兩點同時出發,當P、Q中有一點到達終點時,另一點也停止運動.當t為何值時,直線PQ把△ABC的周長分成相等的兩部分.
【答案】(1)7+![]() ;(2)0<t≤4或t=
;(2)0<t≤4或t=![]() ;(3)t=2,t=6.
;(3)t=2,t=6.
【解析】試題分析:(1)、根據題意得出CP的長度,然后根據勾股定理得出BP的長度,從而得出△ABP的周長;(2)、根據直角三角形的性質得出t的取值范圍;(3)、當P點在AC上,Q在AB上,則PC=t,BQ=2t﹣3,根據周長相等得出t的值;當P點在AB上,Q在AC上,則AC=t﹣4,AQ=2t﹣8,根據周長相等得出t的值.
試題解析:(1)、由∠C=90°,AB=5cm,BC=3cm,
∴AC=4,動點P從點C開始,按C→A→B→C的路徑運動,且速度為每秒1cm, ∴出發2秒后,則CP=2,
∵∠C=90°,∴PB=![]() , ∴△ABP的周長為:AP+PB+AB=
, ∴△ABP的周長為:AP+PB+AB=![]()
(2)、![]()
![]()
(3)、當P點在AC上,Q在AB上,則PC=t,BQ=2t﹣3,
∵直線PQ把△ABC的周長分成相等的兩部分, ∴t+2t﹣3=6, ∴t=2;
當P點在AB上,Q在AC上,則AC=t﹣4,AQ=2t﹣8,
∵直線PQ把△ABC的周長分成相等的兩部分, ∴t﹣4+2t﹣8=6, ∴t=6,
∴當t為2或6秒時,直線PQ把△ABC的周長分成相等的兩部分


科目:初中數學 來源: 題型:
【題目】(本題8分)如圖,在△ABC中,D是BC邊上的一點,∠B=50°,∠BAD=30°,將△ABD沿AD折疊得到△AED,AE與BC交于點F.
(1)求∠AFC的度數;
(2)求∠EDF的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在某次國際乒乓球單打比賽中,甲、乙兩名中國選手進入最后決賽,那么下列事件為必然事件的是( )
A. 冠軍屬于中國選手 B. 冠軍屬于外國選手
C. 冠軍屬于中國選手甲 D. 冠軍屬于中國選手乙
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A.一個游戲的中獎概率是![]() , 則做5次這樣的游戲一定會中獎
, 則做5次這樣的游戲一定會中獎
B.為了解深圳中學生的心理健康情況,應該采用普查的方式
C.事件“小明今年中考數學考95分”是可能事件
D.若甲組數據的方差S![]() =0.01,乙組數據的方差S
=0.01,乙組數據的方差S![]() =0.1,則乙組數據更穩定
=0.1,則乙組數據更穩定
查看答案和解析>>
科目:初中數學 來源: 題型:
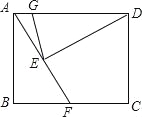
【題目】如圖,在矩形ABCD中,點F在邊BC上,且AF=AD,過點D作DE⊥AF,垂足為點E.以D為圓心,DE為半徑作圓弧交AD于點G,若BF=FC=1,則![]() 的長為 .
的長為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題中,真命題的個數是( )
①過一點有且只有一條直線與已知直線平行;②過一點有且只有一條直線與已知直線垂直;③圖形平移的方向一定是水平的;④內錯角相等;⑤相等的角是對頂角;⑥垂線段最短
A.3B.2C.1D.0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com