
【題目】東坡商貿公司購進某種水果的成本為20元/kg,經過市場調研發現,這種水果在未來48天的銷售單價p(元/kg)與時間t(天)之間的函數關系式為:
 ,且其日銷售量y(kg)與時間t(天)的關系如下表:
,且其日銷售量y(kg)與時間t(天)的關系如下表:

(1)已知y與t之間的變化規律符合一次函數關系,試求在第30天的日銷售量是多少?
(2)問哪一天的銷售利潤最大?最大日銷售利潤為多少?
(3)在實際銷售的前24天中,公司決定每銷售1kg水果就捐贈n元利潤(n<9)給“精準扶貧”對象.現發現:在前24天中,每天扣除捐贈后的日銷售利潤隨時間t的增大而增大,求n的取值范圍.
【答案】(1)y=120-2t,60;(2)在第10天的銷售利潤最大,最大利潤為1250元;(3)7≤n<9.
【解析】
試題分析:(1)根據日銷售量y(kg)與時間t(天)的關系表,設y=kt+b,將表中對應數值代入即可求出k,b,從而求出一次函數關系式,再將t=30代入所求的一次函數關系式中,即可求出第30天的日銷售量.
(2)日銷售利潤=日銷售量×(銷售單價-成本);分1≤t≤24和25≤t≤48兩種情況,按照題目中所給出的銷售單價p(元/kg)與時間t(天)之間的函數關系式分別得出銷售利潤的關系式,再運用二次函數的圖像及性質即可得出結果.
(3)根據題意列出日銷售利潤W=(t+30-20-n)(120-2t)= -t2+2(n+5)t+1200-n,此二次函數的對稱軸為y=2n+10,要使W隨t的增大而增大,2n+10≥24,即可得出n的取值范圍.
試題解析:(1)依題意,設y=kt+b,將(10,100),(20,80)代入y=kt+b,得:![]() ,解得:
,解得:![]() ,∴日銷售量y(kg)與時間t(天)的關系 y=120-2t.當t=30時,y=120-60=60.
,∴日銷售量y(kg)與時間t(天)的關系 y=120-2t.當t=30時,y=120-60=60.
答:在第30天的日銷售量為60千克.
(2)設日銷售利潤為W元,則W=(p-20)y.
當1≤t≤24時,W=(t+30-20)(120-t)=![]() =
=![]()
當t=10時,W最大=1250.
當25≤t≤48時,W=(-t+48-20)(120-2t)=![]() =
=![]()
由二次函數的圖像及性質知:當t=25時,W最大=1085.
∵1250>1085,∴在第10天的銷售利潤最大,最大利潤為1250元.
(3)依題意,得:W=(t+30-20-n)(120-2t)= ![]() ,其對稱軸為y=2n+10,要使W隨t的增大而增大,由二次函數的圖像及性質知:2n+10≥24,解得n≥7.
,其對稱軸為y=2n+10,要使W隨t的增大而增大,由二次函數的圖像及性質知:2n+10≥24,解得n≥7.
又∵n<0,∴7≤n<9.


 孟建平錯題本系列答案
孟建平錯題本系列答案 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案科目:初中數學 來源: 題型:
【題目】在同一平面內三條直線交點有多少個?
甲:同一平面三直線相交交點的個數為0個,因為a∥b∥c,如圖(1)所示.
乙:同一平面內三條直線交點個數只有1個,因為a,b,c交于同一點O,如圖(2)所示.
以上說法誰對誰錯?為什么?
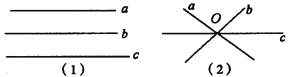
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了測算一塊600畝試驗田里新培育的雜交水稻的產量,隨機對其中的10畝雜交水稻的產量進行了檢測,在這個問題中10是( )
A.個體
B.總體
C.總體的樣本
D.樣本容量
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面每組數分別是三根小木棒的長度,用它們不能擺成一個三角形的是( )
A. 5cm,10cm,5cmB. 7cm,8cm,9cm
C. 3cm,4cm,5cmD. 6cm,20cm,20cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(中考·安徽)如圖,已知反比例函數y=![]() 與一次函數y=k2x+b的圖象交于A(1,8),B(-4,m).
與一次函數y=k2x+b的圖象交于A(1,8),B(-4,m).

(1)求k1,k2,b的值;
(2)求△AOB的面積;
(3)若M(x1,y1),N(x2,y2)是反比例函數y=![]() 的圖象上的兩點,且x1<x2,y1<y2,指出點M,N位于哪個象限,并簡要說明理由.
的圖象上的兩點,且x1<x2,y1<y2,指出點M,N位于哪個象限,并簡要說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】人體中紅細胞的直徑約為0.0000077 m,用科學記數法表示數的結果是( )
A. 0.77×10-5 m B. 0.77×10-6 m
C. 7.7×10-5 m D. 7.7×10-6 m
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com