【題目】閱讀材料，請回答下列問題．
材料一：我國古代數學家秦九韶在《數書九章》中記述了“三斜求積術”，即已知三角形的三邊長，求它的面積，用現代式子表示即為：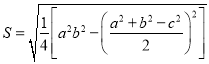
①（其中
為三角形的三邊長，
為面積），而另一個文明古國古希臘也有求三角形面積的“海倫公式”；
……②（其中
）
材料二：對于平方差公式：
公式逆用可得：
，例：
（1）若已知三角形的三邊長分別為4，5，7，請分別運用公式①和公式②，計算該三角形的面積；
（2）你能否由公式①推導出公式②？請試試，寫出推導過程．
快樂5加2金卷系列答案科目：初中數學 來源： 題型：
【題目】計算
(1) 
(2)(2a3b－4ab3)·（－
ab）－(－2a2)2（－b2）
(3)先化簡，再求代數式(a＋2b)(a－2b)＋(a＋2b)2－4ab 的值，其中 a＝1，b＝
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】統計七年級部分同學的跳高測試成績，得到如下頻率直方圖（每組含前一個邊界值，不含后一個邊界值）．
（1）參加測試的總人數是多少人？
（2）組距為多少？
（3）跳高成績在
（含）以上的有多少人？占總人數的百分之幾？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在菱形
中，
，
，點
是
邊的中點，點
是
邊上一動點（不與點
重合），延長
交射線
于點
，連接
，
．
（1）求證：四邊形
是平行四邊形；
（2）填空：
①當
的值為_______時，四邊形是矩形；
②當的值為______時，四邊形是菱形．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀材料：基本不等式
≤
（a＞0，b＞0），當且僅當a＝b時，等號成立．其中我們把叫做正數a、b的算術平均數，叫做正數a、b的幾何平均數，它是解決最大（小）值問題的有力工具．
例如：在x＞0的條件下，當x為何值時，x+
有最小值，最小值是多少？
解：∵x＞0，＞0∴
≥
即是x+≥2
∴x+≥2
當且僅當x＝即x＝1時，x+有最小值，最小值為2．
請根據閱讀材料解答下列問題
（1）若x＞0，函數y＝2x+，當x為何值時，函數有最小值，并求出其最小值．
（2）當x＞0時，式子x2+1+
≥2成立嗎？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
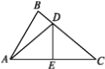
【題目】如圖，已知∠BAC=60° ,∠B=80° ,DE垂直平分AC交BC于點D,交AC于點E.
(1)求∠BAD的度數；
(2)若AB=10,BC=12,求△ABD的周長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】瀘西某著名風景旅游景點于5 月1日前后相繼開放，為了更好的吸引游客前去游覽，某景點給出團體購買公園門票票價如下：
購票人數 | 1～50 | 51～100 | 100人以上 |
每人門票（元） | 13元 | 11元 | 9元 |
今有甲、乙兩個旅行團，已知甲團人數少于50人，乙團人數不超過100人．若分別購票，兩團共計應付門票費1392元，若合在一起作為一個團體購票，總計應付門票費1080元．
（1）請你判斷乙團的人數是否也少于50人．
（2）求甲、乙兩旅行團各有多少人？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在菱形ABCD中，AB=4cm，∠ADC=120°，點E、F同時由A、C兩點出發，分別沿AB、CB方向向點B勻速移動（到點B為止），點E的速度為1cm/s，點F的速度為2cm/s，經過t秒△DEF為等邊三角形，則t的值為 ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
