
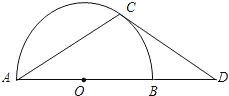
【題目】如圖,點D在⊙O的直徑AB的延長線上,點C在⊙O上,AC=CD,∠D=30°,
(1)求證:CD是⊙O的切線;
(2)若⊙O的半徑為3,求![]() 的長.(結果保留π)
的長.(結果保留π)
 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,∠ABC,∠BCD的平分線BE,CF分別與AD相交于點E、F,BE與CF相交于點G,若AB=3,BC=5,CF=2,則BE的長為( )
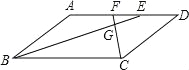
A.2![]() B.4 C.4
B.4 C.4![]() D.5
D.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列每組數分別表示三根木棒的長,將它們首尾連接后,能擺成三角形的一組是( )
A. 2,2,4B. 3,2,6C. 1,2,2D. 1,2,3
查看答案和解析>>
科目:初中數學 來源: 題型:
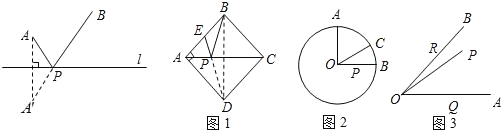
【題目】幾何模型:
條件:如圖,A、B是直線l同旁的兩個定點.
問題:在直線l上確定一點P,使PA+PB的值最小.
方法:作點A關于直線l的對稱點A′,連結A′B交l于點P,則PA+PB=A′B的值最小(不必證明).
模型應用:
(1)如圖1,正方形ABCD的邊長為2,E為AB的中點,P是AC上一動點.連結BD,由正方形對稱性可知,B與D關于直線AC對稱.連結ED交AC于P,則PB+PE的最小值是 ;
(2)如圖2,⊙O的半徑為2,點A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一動點,求PA+PC的最小值;
(3)如圖3,∠AOB=45°,P是∠AOB內一點,PO=10,Q、R分別是OA、OB上的動點,求△PQR周長的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】據報道,2014年6月,恒大集團與阿里巴巴集團實施戰略合作,阿里巴巴注資12億元入股廣州恒大.將數據1200000000用科學記數法表示為( )
A. 1.2×108 B. 12×108 C. 1.2×10﹣9 D. 1.2×109
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A. 形如ax2+bx+c=0的方程叫做一元二次方程
B. (x+1)(x-1)=0是一元二次方程
C. 方程x2-2x=1的常數項為0
D. 一元二次方程中,二次項系數、一次項系數及常數項都不能為0
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點O為Rt△ABC斜邊AB上一點,以OA為半徑的⊙O與BC切于點D,與AC交于點E,連接AD.
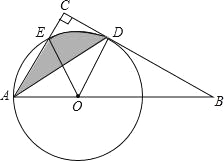
(1)求證:AD平分∠BAC;
(2)若∠BAC=60°,OA=2,求陰影部分的面積(結果保留π).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com