Question

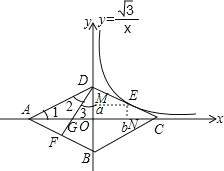
【題目】已知，如圖2菱形ABCD四個頂點都在坐標軸上，對角線AC、BD交于原點O，DF垂直AB交AC于點G，反比例函數，經過線段DC的中點E，若BD=4，則AG的長為（ ）

A． B．+2 C．2+1 D．+1

Answer 1

【答案】A．

【解析】

試題解析：過E作y軸和x的垂線EM，EN，

設E（b，a），

∵反比例函數經過點E，

∴ab=，

∵四邊形ABCD是菱形，

∴BD⊥AC，DO=BD=2，

∵EN⊥x，EM⊥y，

∴四邊形MENO是矩形，

∴ME∥x，EN∥y，

∵E為CD的中點，

∴DOCO=4，

∴CO=2，

∴tan∠DCO=，

∴∠DCO=30°，

∵四邊形ABCD是菱形，

∴∠DAB=∠DCB=2∠DCO=60°，∠1=30°，AO=CO=2，

∵DF⊥AB，

∴∠2=30°，

∴DG=AG，

設DG=r，則AG=r，GO=2-r，

∵AD=AB，∠DAB=60°，

∴△ABD是等邊三角形，

∴∠ADB=60°，

∴∠3=30°，

在Rt△DOG中，DG2=GO2+DO2，

∴r2=（2-r）2+22，

解得：r=，

∴AG=，

故選A．