
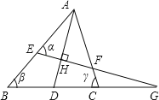
【題目】如圖,AD平分∠BAC,EG⊥AD于H,則下列等式中成立的是 ( )
A. ∠α=![]() (∠β﹣∠γ) B. ∠α=
(∠β﹣∠γ) B. ∠α=![]() (∠β+∠γ) C. ∠G=
(∠β+∠γ) C. ∠G=![]() (∠β+∠γ) D. ∠G=
(∠β+∠γ) D. ∠G=![]() ∠α
∠α
【答案】B
【解析】
由于∠α是△BEC的外角,可以得到∠α=∠β+∠G ①,而∠γ是△CFG的外角,可以得到∠γ=∠CFG+∠G ②,而∠AFE和∠CFG是對頂角,由∠AD平分∠BAC,EG⊥AD于H可以推出∠α=∠AFE,然后利用①②即可得到答案.
∵∠α是△BEC的外角,
∴∠α=∠β+∠G①,
∵∠γ是△CFG的外角,
∴∠γ=∠CFG+∠G②
∵AD平分∠BAC,EG⊥AD于H,AH公共邊,
∴△AEH≌△AFH,
∴AE=AF,
∴∠α=∠AFE,
而∠AFE=∠CFG,
∴∠AFE=∠CFG=∠α,
∴∠γ=∠α+∠G③,
①③得∠α∠γ=∠β∠α,
∴2∠α=∠β+∠γ,
即∠α=![]() (∠β+∠γ).
(∠β+∠γ).
故選:B.


科目:初中數學 來源: 題型:
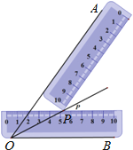
【題目】小明同學在學習了全等三角形的相關知識后發現,只用兩把完全相同的長方形直尺就可以作出一個角的平分線.如圖:一把直尺壓住射線OB,另一把直尺壓住射線OA并且與第一把直尺交于點P,小明說:“射線OP就是∠BOA的角平分線.”他這樣做的依據是( )
A. 角的內部到角的兩邊的距離相等的點在角的平分線上
B. 角平分線上的點到這個角兩邊的距離相等
C. 三角形三條角平分線的交點到三條邊的距離相等
D. 三角形三條垂直平分線的交點到三個定點的距離相等
查看答案和解析>>
科目:初中數學 來源: 題型:
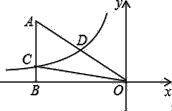
【題目】如圖,已知雙曲線y=![]() (k<0)經過直角三角形OAB斜邊OA的中點D,且與直角邊AB相交于點C.若點A的坐標為(﹣8,4),則△AOC的面積為( )
(k<0)經過直角三角形OAB斜邊OA的中點D,且與直角邊AB相交于點C.若點A的坐標為(﹣8,4),則△AOC的面積為( )
A. 6 B. 12 C. 18 D. 24
查看答案和解析>>
科目:初中數學 來源: 題型:
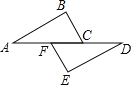
【題目】數學課上,柴老師出了一道題:如圖,已知∠A=∠D,∠BCA=∠EFD.要使△ABC≌△DEF,你還應給出的條件是什么?下面四個同學做了回答:小馬:“增加∠E=∠B;小李:“增加ED=BA;”小周:“增加AB=EF;”小胡:“增加AF=DC.”針對上面四個同學的回答,你認為正確的是_____.(填上你認為正確的同學的名字)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地農民一直保持著冬種油菜的習慣,利用農閑冬種一季油菜.該地農業部門對2017年的油菜籽生產成本、市場價格、種植面積和產量等進行了調查統計,并繪制了如下的統計表與統計圖(如圖):
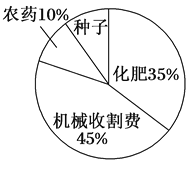
每畝生產成本 | 每畝產量 | 油菜籽市場價格 | 種植面積 |
110元 | 130千克 | 3元/千克 | 500 000畝 |
請根據以上信息解答下列問題:
(1)種植油菜每畝的種子成本是多少元?
(2)農民冬種油菜每畝獲利多少元?
(3)2017年該地全縣農民冬種油菜的總獲利是多少元?(結果用科學記數法表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等腰Rt△ABC中,∠C=90°,D為AC上一點,連接BD,將線段BD繞點D順時針旋轉90°得到線段DE,DE與AB相交于點F,過點D作DG⊥AB,垂足為點G.若EF=5,CD=2 ![]() ,則△BDG的面積為 .
,則△BDG的面積為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等腰Rt△ABC中,∠C=90°,D為AC上一點,連接BD,將線段BD繞點D順時針旋轉90°得到線段DE,DE與AB相交于點F,過點D作DG⊥AB,垂足為點G.若EF=5,CD=2 ![]() ,則△BDG的面積為 .
,則△BDG的面積為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在新晚報舉辦的“萬人戶外徒步活動”中,為統計參加活動人員的年齡情況,從參加人員中隨機抽取了若干人的年齡作為樣本,進行數據統計,制成如圖的條形統計圖和扇形統計圖(部分). 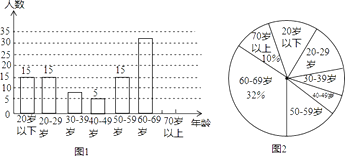
(1)本次活動統計的樣本容量是多少?
(2)求本次活動中70歲以上的人數,并補全條形統計圖;
(3)本次參加活動的總人數約為12000人,請你估算參加活動人數最多的年齡段的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AC=4,BC=7,點D在邊BC上,CD=3,⊙A的半徑長為3,⊙D與⊙A相交,且點B在⊙D外,那么⊙D的半徑長r的取值范圍是( ) 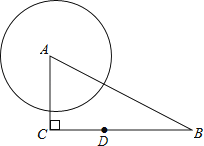
A.1<r<4
B.2<r<4
C.1<r<8
D.2<r<8
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com