
【題目】如圖,在平面直角坐標系中,已知拋物線y=ax2+bx的對稱軸為x=![]() ,且經過點A(2,1),點P是拋物線上的動點,P的橫坐標為m(0<m<2),過點P作PB⊥x軸,垂足為B,PB交OA于點C,點O關于直線PB的對稱點為D,連接CD,AD,過點A作AE⊥x軸,垂足為E.
,且經過點A(2,1),點P是拋物線上的動點,P的橫坐標為m(0<m<2),過點P作PB⊥x軸,垂足為B,PB交OA于點C,點O關于直線PB的對稱點為D,連接CD,AD,過點A作AE⊥x軸,垂足為E.
(1)求拋物線的解析式;
(2)填空:
①用含m的式子表示點C,D的坐標:
C( , ),D( , );
②當m= 時,△ACD的周長最小;
(3)若△ACD為等腰三角形,求出所有符合條件的點P的坐標.
【答案】
(1)
解:(1)依題意,得 ,解得
,解得
∴y=x2﹣![]() x
x
(2)m;![]() ;2m;0;1
;2m;0;1
(3)
依題意,得B(m,0)
在RT△OBC中,OC2=OB2+BC2=m2+![]() =
=![]() m2,
m2,
∴OC=![]() m 又∵O,D關于直線PC對稱,
m 又∵O,D關于直線PC對稱,
∴CD=OC=![]() m
m
在RT△AOE中,OA=![]() =
=![]() =
=![]()
∴AC=OA﹣OC=![]() ﹣
﹣![]() m
m
在RT△ADE中,AD2=AE2+DE2=12+(2﹣2m)2=4m2﹣8m+5
分三種情況討論:
①若AC=CD,即![]() ﹣
﹣![]() m=
m=![]() m,解得m=1,∴P(1,
m,解得m=1,∴P(1,![]() )
)
②若AC=AD,則有AC2=AD2,即5﹣5m+![]() m2=4m2﹣8m+5
m2=4m2﹣8m+5
解得m1=0,m2=![]() .∵0<m<2,∴m=
.∵0<m<2,∴m=![]() ,∴P(
,∴P(![]() ,
,![]() )
)
③若DA=DC,則有DA2=DC2,即4m2﹣8m+5=![]() m2
m2
解得m1=![]() ,m2=2,∵,0<m<2,∴m=
,m2=2,∵,0<m<2,∴m=![]() ,∴P(
,∴P(![]() ,
,![]() )
)
綜上所述,當△ACD為等腰三角形是,點P的坐標分別為P1(1,![]() ),P2(
),P2(![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() ).
).
【解析】(1)根據拋物線對稱軸公式和代入法可得關于a,b的方程組,解方程組可得拋物線的解析式;
(2)①設OA所在的直線解析式為y=kx,將點A(2,1)代入求得OA所在的解析式為y=![]() x,因為PC⊥x軸,所以C得橫坐標與P的橫坐標相同,為m,令x=m,則y=
x,因為PC⊥x軸,所以C得橫坐標與P的橫坐標相同,為m,令x=m,則y=![]() m,所以得出點C(m,
m,所以得出點C(m,![]() m),又點O、D關于直線PB的對稱,所以由中點坐標公式可得點D的橫坐標為2m,則點D的坐標為(2m,0);
m),又點O、D關于直線PB的對稱,所以由中點坐標公式可得點D的橫坐標為2m,則點D的坐標為(2m,0);
②因為O與D關于直線PB的對稱,所以PB垂直平分OD,則CO=CD,因為,△ACD的周長=AC+CD+AD=AC+CO+AD=AO,OA=![]() =
=![]() =
=![]() ,所以當AD最小時,△ACD的周長最小;根據垂線段最短,可知此時點D與E重合,其橫坐標為2,故m=1.
,所以當AD最小時,△ACD的周長最小;根據垂線段最短,可知此時點D與E重合,其橫坐標為2,故m=1.
(3)由中垂線得出CD=OC,再將OC、AC、AD用m表示,然后分情況討論分別得到關于m的方程,解得m,再根據已知條件選取復合體藝的點P坐標即可.
【考點精析】通過靈活運用二次函數的性質,掌握增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小即可以解答此題.


科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c的圖象如圖,點C在y軸的正半軸上,且OA=OC,則( )
A.ac+1=b
B.ab+1=c
C.bc+1=a
D.以上都不是
查看答案和解析>>
科目:初中數學 來源: 題型:
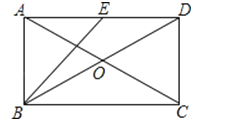
【題目】如圖,在矩形ABCD中,對角線AC,BD相交于點O,E是邊AD的中點.若AC=10,DC=![]() ,則BO= ,∠EBD的大小約為 度 分.(參考數據:tan26°34′≈
,則BO= ,∠EBD的大小約為 度 分.(參考數據:tan26°34′≈![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1的小正方形網格中,三角形的三個頂點均落在格點上.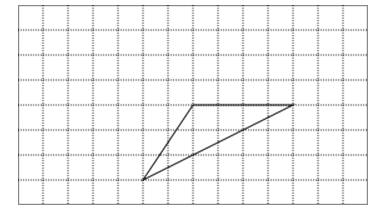
(1)以三角形的其中兩邊為邊畫一個平行四邊形,并在頂點處標上字母A,B,C,D
(2)證明四邊形ABCD是平行四邊形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是半圓O的直徑,C是AB延長線上的一點,CD與半圓O相切于點D,連接AD,BD.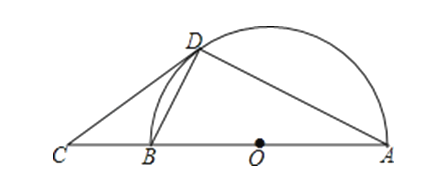
(1)求證:∠BAD=∠BDC;
(2)若∠BDC=28°,BD=2,求⊙O的半徑.(精確到0.01)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某玉米種子的價格為a元/千克,如果一次購買2千克以上的種子,超過2千克部分的種子價格打8折.下表是購買量x(千克)、付款金額y(元)部分對應的值,請你結合表格:
購買量x(千克) | 1.5 | 2 | 2.5 | 3 |
付款金額y(元) | 7.5 | 10 | 12 | b |
(1)寫出a、b的值,a= b= ;
(2)求出當x>2時,y關于x的函數關系式;
(3)甲農戶將18.8元錢全部用于購買該玉米種子,計算他的購買量.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com