【題目】如圖，在Rt△ABC中，∠C= 
，△ACD沿AD折疊，使得點C落在斜邊AB上的點E處．
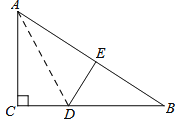
（1）問：△BDE與△BAC相似嗎？
（2）已知AC=6，BC=8，求線段AD的長度．
【答案】
（1）
解答：相似．理由如下：
∵∠C= 
，△ACD沿AD折疊，使得點C落在斜邊AB上的點E處，
∴∠C=∠AED= ，
∴∠DEB=∠C= ，
∵∠B=∠B，
∴△BDE∽△BAC；
（2）
解答：由勾股定理，得
AB= 
=10．
由折疊的性質知，AE=AC=6，DE=CD，∠AED=∠C= ．
∴BE=AB-AE=10-6=4，
在Rt△BDE中，由勾股定理得，
，
即 
，
解得：CD=3，
在Rt△ACD中，由勾股定理得 
即 
，
解得：AD=3
【解析】根據折疊的性質得出∠C=∠AED= ，利用∠DEB=∠C ， ∠B=∠B證明三角形相似；先由勾股定理求出AB的長，再由折疊的性質知DE=CD ， AE=AC ， BE=AB-AE ， 在Rt△BDE中運用勾股定理求出DE ， 即CD ， 最后在Rt△ACD中運用勾股定理得出AD ．
【考點精析】解答此題的關鍵在于理解勾股定理的概念的相關知識，掌握直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2，以及對翻折變換（折疊問題）的理解，了解折疊是一種對稱變換，它屬于軸對稱，對稱軸是對應點的連線的垂直平分線，折疊前后圖形的形狀和大小不變，位置變化，對應邊和角相等．
科目：初中數學 來源： 題型：
【題目】如圖，在3×3正方形網格中，頂點是網格線的交點的三角形叫做格點三角形，給出下列命題： ①一定存在全等的兩個格點三角形
②一定存在相似且不全等的兩個格點三角形
③一定存在兩個格點三角形是位似圖形
④一定存在周長和面積均為無理數的格點三角形
其中真命題的個數是（ ）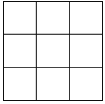
A.4個
B.3個
C.2個
D.1個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，點A(4，0)，B(0，3)，以線段AB為邊在第一象限內作等腰直角三角形ABC，∠BAC＝90°.若第二象限內有一點P
，且△ABP的面積與△ABC的面積相等．
(1)求直線AB的函數表達式．
(2)求a的值．
(3)在x軸上是否存在一點M，使△MAC為等腰三角形？若存在，直接寫出點M的坐標；若不存在，請說明理由．
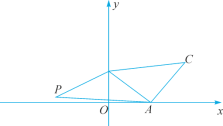
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知y－2與x+1成正比例函數關系，且x=－2時，y=6.
（1）寫出y與x之間的函數解析式；
（2）求當x=－3時，y的值；
（3）求當y=4時，x的值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）將下列各數填在相應的大括號里：
﹣50%，2014，0.61，﹣3，﹣
，0，5.9，﹣3.14，﹣92
整數：{ ，… }
分數：{ ，… }
負分數：{ ，… }
（2）在（1）的數據中，最大的整數是 ，最小的分數是 .
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在我市美化工程招標時，有甲、乙兩個工程隊投標．經測算：甲隊單獨完成這項工程需要60天；若由甲隊先做20天，剩下的工程由甲、乙合做24天可完成．
（1）乙隊單獨完成這項工程需要多少天？
（2）甲隊施工一天，需付工程款3.5萬元，乙隊施工一天需付工程款2萬元．若該工程計劃在70天內完成，在不超過計劃天數的前提下，是由甲隊或乙隊單獨完成該工程省錢？還是由甲乙兩隊全程合作完成該工程省錢？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲、乙兩商場自行定價銷售某一商品．
（1）甲商場將該商品提價15%后的售價為1.15元，則該商品在甲商場的原價為 ▲ 元；
（2）乙商場將該商品提價20%后，用6元錢購買該商品的件數比沒提價前少買1件，求該商品在乙商場的原價是多少？
（3）在（1）、（2）小題的條件下，甲、乙兩商場把該商品均按原價進行了兩次價格調整．
甲商場：第一次提價的百分率是
，第二次提價的百分率是
；
乙商場：兩次提價的百分率都是
(
．
請問甲、乙兩商場，哪個商場的提價較多？請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】觀察下列計算過程，發現規律，利用規律猜想并計算：
1+2=
=3；1+2+3=
=6，1+2+3+4=
=10；1+2+3+4+5=
=15；…
（1）猜想：1+2+3+4+…+n= ．
（2）利用上述規律計算：1+2+3+4+…+200；
（3）嘗試計算：3+6+9+12+…3n的結果．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，△ABC的邊BC的中垂線DM交∠BAC的平分線AD于D， DE⊥AB于點E，DF⊥AC于F.連接DB、DC
（1）求證：△DBE≌△DFC.
（2）求證：AB+AC=2AE
（3）如圖2，若△ABC的邊BC的中垂線DM交∠BAC的外角平分線AD于D， DE⊥AB于點E，且AB>AC，寫出AE、BE、AC之間的等量關系。（不需證明，只需在圖2中作出輔助線、說明證哪兩個三角形全等即可）。
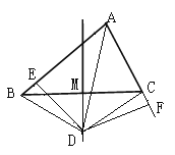
圖1 圖2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com