
【題目】二次函數y=﹣(x﹣2)2+ ![]() 的圖象與x軸圍成的封閉區域內(包括邊界),橫、縱坐標都是整數的點有個(提示:必要時可利用下面的備用圖畫出圖象來分析).
的圖象與x軸圍成的封閉區域內(包括邊界),橫、縱坐標都是整數的點有個(提示:必要時可利用下面的備用圖畫出圖象來分析). 
 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:初中數學 來源: 題型:
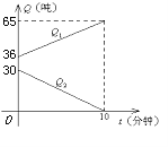
【題目】某軍加油飛機接到命令,立即給另一架正在飛行的運輸飛機進行空中加油.在加油的過程中,設運輸飛機的油箱余油量為Q1噸,加油飛機的加油油箱的余油量為Q2噸,加油時間為t分鐘,Q1、Q2與t之間的函數關系如圖.回答問題:
(1) 加油飛機的加油油箱中裝載了多少噸油?將這些油全部加給運輸飛機需要多少分鐘?
(2) 求加油過程中,運輸飛機的余油量Q1(噸)與時間t(分鐘)的函數關系式;
(3) 運輸飛機加完油后,以原速繼續飛行,需10小時到達目的地,油料是否夠用?
請通過計算說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AD是△ABC的中線,E,F分別是AD和AD延長線上的點,且DE=DF,連接BF、CE,且∠FBD=35°,∠BDF=75°,下列說法:①△BDF≌CDE;②ABD和△ACD面積相等;③BF∥CE;④∠DEC=70°,其中正確的有( )
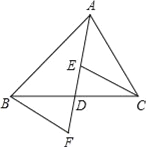
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某出租車駕駛員從公司出發,在南北向的人民路上連續接送5批客人,行駛路程記錄如下(規定向南為正,向北為負,單位:km):

①接送完第5批客人后,該駕駛員在公司什么方向,距離公司多少千米?
②若該出租車每千米耗油0.2升,那么在這過程中共耗油多少升?
③若該出租車的計價標準為:行駛路程不超過3km收費10元,超過3km的部分按每千米加1.8元收費,在這過程中該駕駛員共收到車費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在△ABC中,D是BA延長線上一點,AE是∠DAC的平分線,P是AE上的一點(點P不與點A重合),連接PB,PC.通過觀察,測量,猜想PB+PC與AB+AC之間的大小關系,并加以證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在實踐中學習:
(1)如圖1所示:已知AB∥CD,∠ABD=115°,根據 可得出:∠BDC的度數是 .
(2)如圖2所示:已知AB∥CD,∠ABC=25°,∠EDC=40°,求∠BED的度數.
(3)如圖3所示:已知MA∥NC,試確定∠A、∠B、∠C和∠E、∠F的關系,并說明理由.
(4)如圖4所示:已知AB∥CD,∠ABE=α,∠FCD=β,∠CFE=γ,且BE⊥EF,試確定α、β、γ的關系,請說明理由.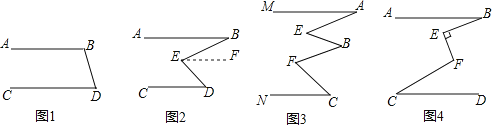
查看答案和解析>>
科目:初中數學 來源: 題型:
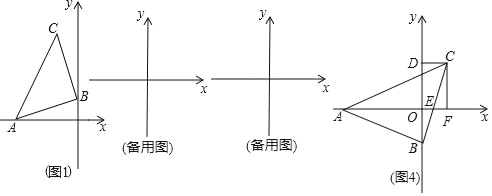
【題目】如圖,△ABC為等腰直角三角形,∠ABC=90°,AB=BC,點A在x軸的負半軸上,點B是y軸上的一個動點,點C在點B的上方,
(1)如圖1當點A的坐標為(﹣3,0),點B的坐標為(0,1)時,求點C的坐標;
(2)設點A的坐標為(a,0),點B的坐標為(0,b).過點C作CD⊥y軸于點D,在點B運動過程中(不包含△ABC的一邊與坐標軸重合的情況),猜想線段OD的長與a、b的數量關系,并說明理由;
(3)在(2)的條件下如圖4,當x軸平分∠BAC時,BC交x軸于點E,過點作CF⊥x軸于點F.說明此時線段CF與AE的數量關系(用含a、b的式子表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AE是△ABC的角平分線,AD⊥BC于點D,若∠BAC=128°,∠C=36°,則∠DAE的度數是( ) 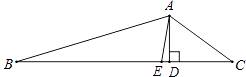
A.10°
B.12°
C.15°
D.18°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com