
【題目】如圖,在x軸的上方,直角∠BOA繞原點O按順時針方向旋轉,若∠BOA的兩邊分別與函數y=﹣![]() 、y=
、y=![]() 的圖象交于B、A兩點,則∠OAB的大小的變化趨勢為( )
的圖象交于B、A兩點,則∠OAB的大小的變化趨勢為( )
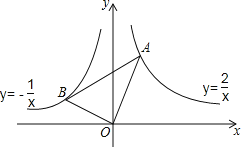
A.逐漸變小 B.逐漸變大 C.時大時小 D.保持不變
【答案】D
【解析】
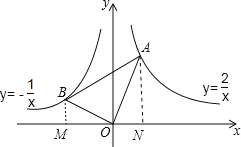
試題分析:如圖,作輔助線;首先證明△BOM∽△OAN,得到![]() ;設B(﹣m,
;設B(﹣m,![]() ),A(n,
),A(n,![]() ),得到BM=
),得到BM=![]() ,AN=
,AN=![]() ,OM=m,ON=n,進而得到mn=
,OM=m,ON=n,進而得到mn=![]() ,mn=
,mn=![]() ,此為解決問題的關鍵性結論;運用三角函數的定義證明知tan∠OAB=
,此為解決問題的關鍵性結論;運用三角函數的定義證明知tan∠OAB=![]() 為定值,即可解決問題.
為定值,即可解決問題.
解:如圖,分別過點A、B作AN⊥x軸、BM⊥x軸;
∵∠AOB=90°,
∴∠BOM+∠AON=∠AON+∠OAN=90°,
∴∠BOM=∠OAN,
∵∠BMO=∠ANO=90°,
∴△BOM∽△OAN,
∴![]() ;
;
設B(﹣m,![]() ),A(n,
),A(n,![]() ),
),
則BM=![]() ,AN=
,AN=![]() ,OM=m,ON=n,
,OM=m,ON=n,
∴mn=![]() ,mn=
,mn=![]() ;
;
∵∠AOB=90°,
∴tan∠OAB=![]() ①;
①;
∵△BOM∽△OAN,
∴![]() =
=![]() =
=![]() =
=![]() ②,
②,
由①②知tan∠OAB=![]() 為定值,
為定值,
∴∠OAB的大小不變,
故選:D.


科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=﹣x+m的圖象和y軸交于點B,與正比例函數y=![]() x圖象交于點P(2,n).
x圖象交于點P(2,n).
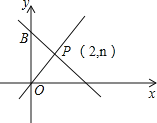
(1)求m和n的值;
(2)求△POB的面積.
考點:兩條直線相交或平行問題;二元一次方程組的解.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2015年10月18日,TCL2015長沙國際馬拉松賽正式開賽,來自國內外的1.5萬余名選手在長沙這座美麗的城市中奔跑.馬拉松長跑是國際上非常普及的長跑比賽項目,全程距離約為42千米,將數據42千米用科學記數法表示為( )
A. 42×103米 B. 0.42×105米 C. 4.2×104米 D. 4.2×105米
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com