
【題目】如圖,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() (
(![]() 為常數,且
為常數,且![]() )的圖象交于A(1,a)、B兩點.
)的圖象交于A(1,a)、B兩點.
(1)求反比例函數的表達式及點B的坐標;
(2)在x軸上找一點P,使PA+PB的值最小,求滿足條件的點P的坐標及△PAB的面積.

【答案】(1)![]() ,B(3,1);(2)P(
,B(3,1);(2)P(![]() ,0),
,0),![]() .
.
【解析】
試題分析:(1)把點A(1,a)代入一次函數y=﹣x+4,即可得出a,再把點A坐標代入反比例函數![]() ,即可得出k,兩個函數解析式聯立求得點B坐標;
,即可得出k,兩個函數解析式聯立求得點B坐標;
(2)作點B作關于x軸的對稱點D,交x軸于點C,連接AD,交x軸于點P,此時PA+PB的值最小,求出直線AD的解析式,令y=0,即可得出點P坐標.
試題解析:(1)把點A(1,a)代入一次函數y=﹣x+4,得a=﹣1+4,解得a=3,∴A(1,3),點A(1,3)代入反比例函數![]() ,得k=3,∴反比例函數的表達式
,得k=3,∴反比例函數的表達式![]() ,兩個函數解析式聯立列方程組得
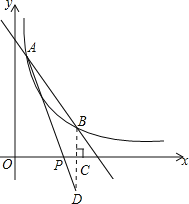
,兩個函數解析式聯立列方程組得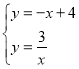 ,解得
,解得![]() 或
或![]() ,∴點B坐標(3,1);
,∴點B坐標(3,1);
(2)作點B作關于x軸的對稱點D,交x軸于點C,連接AD,交x軸于點P,此時PA+PB的值最小,∴D(3,﹣1),設直線AD的解析式為y=mx+n,把A,D兩點代入得,![]() ,解得m=﹣2,n=5,∴直線AD的解析式為y=﹣2x+5,令y=0,得x=
,解得m=﹣2,n=5,∴直線AD的解析式為y=﹣2x+5,令y=0,得x=![]() ,∴點P坐標(
,∴點P坐標(![]() ,0),S△PAB=S△ABD﹣S△PBD=
,0),S△PAB=S△ABD﹣S△PBD=![]() ×2×2﹣
×2×2﹣![]() ×2×
×2×![]() =2﹣
=2﹣![]() =1.5.
=1.5.


科目:初中數學 來源: 題型:
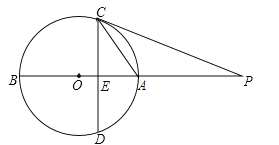
【題目】如圖,AB是⊙O的直徑,點P在BA的延長線上,弦CD⊥AB,垂足為E,且![]() =PEPO.
=PEPO.
(1)求證:PC是⊙O的切線.
(2)若OE:EA=1:2,PA=6,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,P為反比例函數y= ![]() 的圖像上一點,PA⊥x軸于點A,△PAO的面積為6,則下列各點中也在這個反比例函數圖像上的是( )
的圖像上一點,PA⊥x軸于點A,△PAO的面積為6,則下列各點中也在這個反比例函數圖像上的是( ) 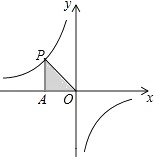
A.(2,3)
B.(﹣2,6)
C.( 2,6 )
D.(﹣2,3)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程(a﹣1)x2﹣2x+1=0有兩個不相等的實數根,則a的取值范圍是( )
A.a<2
B.a>2
C.a<﹣2
D.a<2且a≠1
查看答案和解析>>
科目:初中數學 來源: 題型:
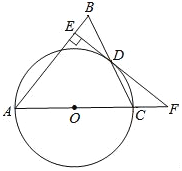
【題目】如圖,在△ABC中,AB=AC,以AC邊為直徑作⊙O交BC邊于點D,過點D作DE⊥AB于點E,ED、AC的延長線交于點F.
(1)求證:EF是⊙O的切線;
(2)若EB=![]() ,且sin∠CFD=
,且sin∠CFD=![]() ,求⊙O的半徑與線段AE的長.
,求⊙O的半徑與線段AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
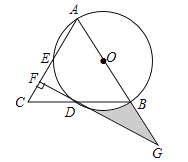
【題目】如圖,在△ABC中,AB=AC,以AB為直徑的⊙O分別交線段BC,AC于點D,E,過點D作DF⊥AC,垂足為F,線段FD,AB的延長線相交于點G.
(1)求證:DF是⊙O的切線;
(2)若CF=1,DF=![]() ,求圖中陰影部分的面積.
,求圖中陰影部分的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com