
【題目】如圖,正方形ABCD中,點E、F分別在BC、CD上,△AEF是等邊三角形,連結AC交EF于G,下列結論:①BE=DF;②∠AEF=15°;③AC垂直平分EF;④BE+DF=EF;⑤△CEF為等腰直角三角形,其中正確的有(填序號). 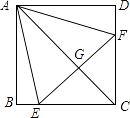
【答案】①③⑤
【解析】解:∵四邊形ABCD是正方形,△AEF是等邊三角形, ∴AB=AD,AE=AF,∠B=∠D,=90°,
在Rt△ABE和Rt△ADF中, ![]() ,
,
∴Rt△ABE≌Rt△ADF,
∴BE=DF,故①正確,
∵BC=DC,
∴CE=CF,
∴⑤△CEF為等腰直角三角形,
由于AE=AF,CW=CF,
∴AC垂直平分EF,故③⑤正確,
∵△AEF是等邊三角形,∴∠AEF=60°,故②錯誤,
設EC=x,由勾股定理,得
EF= ![]() x,CG=
x,CG= ![]() x,
x,
AG=AEsin60°=EFsin60°=2×CGsin60°= ![]() x,
x,
∴AC= ![]() ,
,
∴AB= ![]() ,
,
∴BE= ![]() ﹣x=
﹣x= ![]() ,
,
∴BE+DF= ![]() x﹣x≠
x﹣x≠ ![]() x,故④錯誤,
x,故④錯誤,
所以答案是:①③⑤.
【考點精析】根據題目的已知條件,利用等腰直角三角形和線段垂直平分線的性質的相關知識可以得到問題的答案,需要掌握等腰直角三角形是兩條直角邊相等的直角三角形;等腰直角三角形的兩個底角相等且等于45°;垂直于一條線段并且平分這條線段的直線是這條線段的垂直平分線;線段垂直平分線的性質定理:線段垂直平分線上的點和這條線段兩個端點的距離相等.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】下列事件中,是必然事件的是( )
A.購買一張彩票,中獎B.射擊運動員射擊一次,命中靶心
C.任意畫一個三角形,其內角和是180°D.經過有交通信號燈的路口,遇到紅燈
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC的三個頂點的坐標分別為A(-2,3)、B(-6,0)、C(-1,0).
(1)請直接寫出點A關于原點O對稱的點的坐標;
(2)將△ABC繞坐標原點O逆時針旋轉90°,畫出圖形,寫出點B的對應點的坐標;
(3)請直接寫出:以A、B、C為頂點的平行四邊形的第四個頂點D的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AD∥BC,BA⊥AD,BC=DC,BE⊥CD于點E. 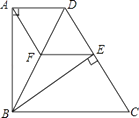
(1)求證:△ABD≌△EBD;
(2)過點E作EF∥DA,交BD于點F,連接AF.求證:四邊形AFED是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】畫圖并計算:已知線段AB=2 cm,延長線段AB至點C,使得2BC=AB,再反向延長AC至點D,使得AD=AC.
(1)準確地畫出圖形,并標出相應的字母;
(2)線段DC的中點是哪個?線段AB的長是線段DC長的幾分之幾?
(3)求出線段BD的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將多項式x3﹣5xy2﹣7y3+8x2y按某一個字母的升冪排列,正確的是( )
A.x3﹣7y3﹣5xy2+8x2y
B.﹣7y3﹣5xy2+8x2y+x3
C.7y3﹣5xy2+8x2y+x3
D.x3﹣5xy2+8x2y﹣7y3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,數軸上點A、B所表示的數分別是4,8,
(1)請用尺規作圖的方法確定原點O的位置(不寫做法,保留作圖痕跡)
(2)已知動點M從點A出發,以每秒1個單位長度的速度沿數軸向左勻速運動,同時點N從點A出發,以每秒2個單位長度的速度沿數軸向右勻速運動,設運動時間為t(t>0)秒.
①運動1秒后,點M表示的數是_____,點N表示的數為______
②運動t秒后,點M表示的數是_____,點N表示的數為______
③若線段BN=2,求此時t的大小以及相應的M所表示的數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四邊形ABCD中,對角線AC、BD相交于點O,下列條件不能判定這個四邊形是平行四邊形的是( ) 
A.AB∥DC,AD∥BC
B.AB=DC,AD=BC
C.AO=CO,BO=DO
D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,BC是⊙O的直徑,A是⊙O上一點,過點B作⊙O的切線,與CA的延長線相交于點E,F是BE的中點,延長AF與CB的延長線相交于點P.
(1)求證:PA是⊙O的切線;
(2)如圖2,若AD⊥BC于點D,連接CF與AD相交于點G.求證:AG=GD;
(3)在(2)的條件下,若FG=BF,且⊙O的半徑長為![]() ,求BD的長度.
,求BD的長度.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com