
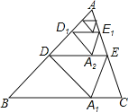
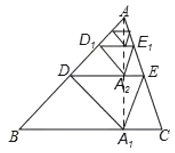
【題目】如圖,將△ABC沿著過AB中點D的直線折疊,使點A落在BC邊上的A1,稱為第1次操作,折痕DE到BC的距離記為h1;還原紙片后,再將△ADE沿著過AD中點D1的直線折疊,使點A落在DE邊上的A2處,稱為第2次操作,折痕D1E1到BC的距離記為h2:按上述方法不斷操作下去…,經過第2019次操作后得到的折痕D2018E2018,到BC的距離記為h2019:若h1=1,則h2019的值為(____)
【答案】2﹣![]()
【解析】
根據中點的性質及折疊的性質可得DA=DA'=DB,從而可得∠ADA'=2∠B,結合折疊的性質可得∠ADA'=2∠ADE,可得∠ADE=∠B,繼而判斷DE∥BC,得出DE是△ABC的中位線,證得AA1⊥BC,得到AA1=2,求出h1=21=1,同理,h2=2![]() ,h3=2
,h3=2![]() ×
×![]() =2
=2![]() ,經過第n次操作后得到的折痕Dn1En1到BC的距離hn=2
,經過第n次操作后得到的折痕Dn1En1到BC的距離hn=2![]() .
.
解:由折疊的性質可得:AA1⊥DE,DA=DA1,
又∵D是AB中點,
∴DA=DB,
∴DB=DA1,
∴∠BA1D=∠B,
∴∠ADA1=2∠B,
又∵∠ADA1=2∠ADE,
∴∠ADE=∠B,
∴DE∥BC,
∴AA1⊥BC,
∴AA1=2h1=2,
∴h1=21=1,
同理,h2=2![]() ,h3=2
,h3=2![]() ×
×![]() =2
=2![]() …
…
∴經過第n次操作后得到的折痕Dn1En1到BC的距離hn=2![]() ,
,
∴h2019=2![]() .
.
故答案為:2![]() .
.


 教學練新同步練習系列答案
教學練新同步練習系列答案 課前課后同步練習系列答案
課前課后同步練習系列答案 課堂小作業系列答案
課堂小作業系列答案 黃岡小狀元口算速算練習冊系列答案
黃岡小狀元口算速算練習冊系列答案 成功訓練計劃系列答案
成功訓練計劃系列答案 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案科目:初中數學 來源: 題型:
【題目】如圖,一個長方形運動場被分隔成A,B,A,B,C共5個區,A區是邊長為a m的正方形,C區是邊長為c m的正方形.
(1)列式表示每個B區長方形場地的周長,并將式子化簡;
(2)列式表示整個長方形運動場的周長,并將式子化簡;
(3)如果a=40,c=10,求整個長方形運動場的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著通訊市場競爭的日益激烈,為了占領市場,甲公司推出的優惠措施是:每分鐘降低![]() 元后,再下調
元后,再下調![]() ;乙公司推出的優惠措施是:每分鐘下調
;乙公司推出的優惠措施是:每分鐘下調![]() 后,再降低
后,再降低![]() 元.已知甲、乙兩公司原來每分鐘收費標準相同,都是
元.已知甲、乙兩公司原來每分鐘收費標準相同,都是![]() 元.
元.
(1)用含![]() ,
,![]() 的式子表示甲、乙兩公司推出優惠措施后每分鐘的收費標準;
的式子表示甲、乙兩公司推出優惠措施后每分鐘的收費標準;
(2)推出優惠措施后哪家公司的收費便宜?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖所示,線段![]() ,點
,點![]() 是線段
是線段![]() 上一點,
上一點,![]() 分別是線段
分別是線段![]() 的中點,小明據此很輕松地求得
的中點,小明據此很輕松地求得![]() ;你知道小明是怎樣求出來的嗎?請寫出求解過程.
;你知道小明是怎樣求出來的嗎?請寫出求解過程.
![]()
(2)小明反思過程中突發奇想:若點![]() 在
在![]() 的延長線上時,原有的結論“
的延長線上時,原有的結論“![]() ”是否仍然成立?請幫小明畫出圖形并說明理由.
”是否仍然成立?請幫小明畫出圖形并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
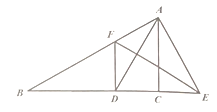
【題目】如圖所示,在![]() 中,
中,![]() 是
是![]() 平分線,
平分線,![]() 的垂直平分線分別交
的垂直平分線分別交![]() 延長線于點
延長線于點![]() .求證:
.求證:![]() .
.
證明:∵![]() 平分
平分![]()
∴![]()
![]() (角平分線的定義)
(角平分線的定義)
∵![]() 垂直平分
垂直平分![]()
∴ ![]() (線段垂直平分線上的點到線段兩個端點距離相等)
(線段垂直平分線上的點到線段兩個端點距離相等)
∴![]() ( )
( )
∴![]() (等量代換)
(等量代換)
∴![]() ( )
( )
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一塊長5米寬4米的地毯,為了美觀設計了兩橫、兩縱的配色條紋(圖中陰影部分),已知配色條紋的寬度相同,所占面積是整個地毯面積的![]() .
.
(1)求配色條紋的寬度;
(2)如果地毯配色條紋部分每平方米造價200元,其余部分每平方米造價100元,求地毯的總造價.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC中,AB=AC=10cm,BC=8cm,點D為AB的中點.如果點P在線段BC上以3cm/s的速度由點B向C點運動,同時,點Q在線段CA上由點C向A點運動.
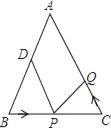
(1)若點Q的運動速度與點P的運動速度相等,經過1秒后,△BPD與△CQP是否全等,請說明理由.
(2)若點Q的運動速度與點P的運動速度不相等,當點Q的運動速度為多少時,能夠使△BPD與△CQP全等?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com