
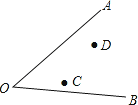
【題目】已知:∠AOB和兩點C、D,求作一點P,使PC=PD,且點P到∠AOB的兩邊的距離相等.
(要求:用尺規作圖,保留作圖痕跡,寫出作法,不要求證明).
【答案】

【解析】
試題分析:由所求的點P滿足PC=PD,利用線段垂直平分線定理得到P點在線段CD的垂直平分線上,再由點P到∠AOB的兩邊的距離相等,利用角平分線定理得到P在∠AOB的角平分線上,故作出線段CD的垂直平分線,作出∠AOB的角平分線,兩線交點即為所求的P點.
試題解析:如圖所示:

作法:(1)以O為圓心,任意長為半徑畫弧,與OA、OB分別交于兩點;
(2)分別以這兩交點為圓心,大于兩交點距離的一半長為半徑,在角內部畫弧,兩弧交于一點;
(3)以O為端點,過角內部的交點畫一條射線;
(4)連接CD,分別為C、D為圓心,大于![]() CD長為半徑畫弧,分別交于兩點;
CD長為半徑畫弧,分別交于兩點;
(5)過兩交點畫一條直線;
(6)此直線與前面畫的射線交于點P,
∴點P為所求的點.


科目:初中數學 來源: 題型:
【題目】若A(﹣4,y1),B(﹣3,y2),C(1,y3)為二次函數y=x2+4x﹣5的圖象上的三點,則y1,y2,y3的大小關系是( )
A. y1<y2<y3 B. y2<y1<y3 C. y3<y1<y2 D. y1<y3<y2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(8分)我市中學組籃球比賽中,每場比賽都要分出勝負,每隊勝1場得2分,負1場得1分.某隊為了爭取較好名次,想在全部22場比賽中得到40分,那么這個隊勝負場數分別是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某單位人事部欲從內部招聘管理人員一名,對甲、乙、丙三名候選人進行專業知識測試,成績如下表所示;并依錄用的程序,組織200名職工對三人進行民主評議投票推薦,三人得票率如圖所示.(沒有棄權票,每位職工只能投1票,每得1票記作1分)
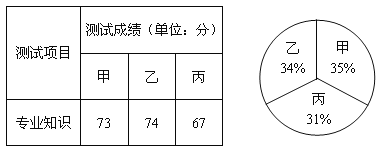
(1)請填出三人的民主評議得分:甲得 分,乙得 分,丙得 分;
(2)根據招聘簡章,人事部將專業知識、民主評議二項得分按6:4的比例確定各人成績,成績優者將被錄用.那么 將被錄用,他的成績為 分.
查看答案和解析>>
科目:初中數學 來源: 題型:
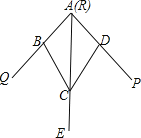
【題目】如圖,小敏做了一個角平分儀ABCD,其中AB=AD,BC=DC.將儀器上的點A與∠PRQ的頂點R重合,調整AB和AD,使它們分別落在角的兩邊上,過點A,C畫一條射線AE,AE就是∠PRQ的平分線.此角平分儀的畫圖原理是:根據儀器結構,可得△ABC≌△ADC,這樣就有∠QAE=∠PAE.則說明這兩個三角形全等的依據是( )
A.SAS
B.ASA
C.AAS
D.SSS
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,AB=6,點E在邊CD上,且CD=3DE.將△ADE 沿AE對折至△AFE,延長EF交邊BC于點G,連接AG,CF.
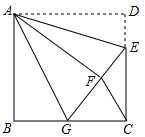
求證:(1)△ABG≌△AFG;
(2)求△FGC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知矩形ABCD的長AB為5,寬BC為4,E是BC邊上的一個動點,AE⊥EF,EF交CD于點F.設BE=x,FC=y,則點E從點B運動到點C時,能表示y關于x的函數關系的大致圖象是( )

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班將安全知識競賽成績整理后繪制成直方圖,圖中從左至右前四組的百分比分別是4%,12%,40%,28%,第五組的頻數是8.則:① 該班有50名同學參賽;② 第五組的百分比為16%;③ 成績在70~80分的人數最多;④ 80分以上的學生有14名,其中正確的個數有( )
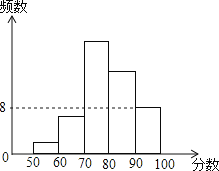
A.1個 B.2個 C.3個 D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com