
【題目】在△ABC中,AB=AC,D是線段BC的延長線上一點,以AD為一邊在AD的右側作△ADE,使AE=AD,∠DAE=∠BAC,連接CE.
(1)如圖,點D在線段BC的延長線上移動,若∠BAC=40![]() ,則∠DCE=
,則∠DCE= ![]() .
.
(2)設∠BAC=m,∠DCE=n.
①如圖,當點D在線段BC的延長線上移動時,m與n之間有什么數量關系?請說明理由.
②當點D在直線BC上(不與B、C重合)移動時,m與n之間有什么數量關系?請直接寫出你的結論.

【答案】(1)40;(2)①m=n,理由見解析;②m+n=180°
【解析】試題分析:(1)可證△ABD≌△ACE,可得∠ACE=∠B,即可解題;
(2)①根據△ABD≌△ACE可分別求得∠BCE用m和用n分別表示,即可求得m、n的關系;②分兩種情況分析,第1種,當D在線段BC的延長線上或反向延長線上時,第2種,當D在線段BC上時.
試題解析:(1)∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
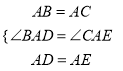 ,
,
∴△ABD≌△ACE(SAS),
∴∠ACE=∠B,
∵AB=AC,∠BAC=40°,
∴∠ACE=∠B=70°,
∴∠DCE=180°70°70°=40°;
(2) ①∵△ABD≌△ACE(1)已證,
∴∠ACE=∠B,
∵AB=AC,∠BAC=m,
∴∠ACE=∠B=∠ACB=![]() ,
,
∴∠BCE=∠ACB+∠ACE=180°m,
∵∠BCE=180°∠DCE=180°n,
∴m=n.
②當D在線段BC的延長線上或反向延長線上時,m=n,
當D在線段BC上時,m+n=180°.


科目:初中數學 來源: 題型:
【題目】閱讀下面材料,并解答問題.
將分式![]() 拆分成一個整式與一個分式(分子為整數)的和的形式.
拆分成一個整式與一個分式(分子為整數)的和的形式.
解:由分母為x2-1,可設x4+x2-3=(x2-1)(x2+a)+b.
則x4+x2-3=(x2-1)(x2+a)+b=x4-x2+ax2-a+b=x4+(a-1)x2-a+b
∴![]() ,∴
,∴![]()
∴![]()
這樣,分式![]() 被拆分成了一個整式x2+2與一個分式-
被拆分成了一個整式x2+2與一個分式-![]() 的和.
的和.
根據上述作法,將分式![]() 拆分成一個整式與一個分式(分子為整數)的和的形式。
拆分成一個整式與一個分式(分子為整數)的和的形式。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一個正比例函數圖象與一個一次函數圖象交于點A(3,4),且一次函數的圖象與y軸相交于點B(0,-5).

(1)求這兩個函數的表達式;
(2)求△AOB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知反比例函數![]() ,(k為常數,k≠1).
,(k為常數,k≠1).
(1)若點A(1,2)在這個函數的圖象上,求k的值;
(2)若在這個函數圖象的每一分支上,y隨x的增大而增大,求k的取值范圍;
(3)若k=13,試判斷點B(3,4),C(2,5)是否在這個函數的圖象上,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
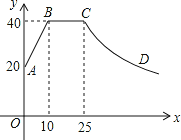
【題目】心理學家研究發現,一般情況下,一節課40分鐘中,學生的注意力隨教師講課的變化而變化.開始上課時,學生的注意力逐步增強,中間有一段時間學生的注意力保持較為理想的穩定狀態,隨后學生的注意力開始分散.經過實驗分析可知,學生的注意力指數y隨時間x(分鐘)的變化規律如下圖所示(其中AB、BC分別為線段,CD為雙曲線的一部分):
(1)求出線段AB,曲線CD的解析式,并寫出自變量的取值范圍;
(2)開始上課后第五分鐘時與第三十分鐘時相比較,何時學生的注意力更集中?
(3)一道數學競賽題,需要講19分鐘,為了效果較好,要求學生的注意力指數最低達到36,那么經過適當安排,老師能否在學生注意力達到所需的狀態下講解完這道題目?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=x+1與y軸交于A點,與反比例函數![]() (x>0)的圖象交于點M,過M作MH⊥x軸于點H,且
(x>0)的圖象交于點M,過M作MH⊥x軸于點H,且![]() .
.
(1)求k的值;
(2)設點N(1,a)是反比例函數![]() (x>0)圖象上的點,在y軸上是否存在點P,使得PM+PN最小?若存在,求出點P的坐標;若不存在,請說明理由.
(x>0)圖象上的點,在y軸上是否存在點P,使得PM+PN最小?若存在,求出點P的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,以AB為直徑的⊙O分別與BC,AC相交于點D,E,BD=CD,過點D作⊙O的切線交邊AC于點F.
(1)求證:DF⊥AC;
(2)若⊙O的半徑為5,∠CDF=30°,求![]() 的長(結果保留π).
的長(結果保留π).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com