
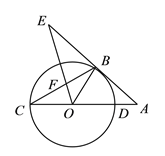
【題目】如圖, ![]() 為⊙
為⊙![]() 的直徑,點
的直徑,點![]() 在⊙
在⊙![]() 上,連接
上,連接![]() 、
、![]() ,過點
,過點![]() 的切線
的切線![]() 與
與![]() 的延長線交于點
的延長線交于點![]() ,
, ![]() ,交
,交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() .
.
(![]() )求證:
)求證: ![]() .
.
(![]() )若⊙
)若⊙![]() 的半徑為
的半徑為![]() ,
, ![]() ,求
,求![]() 的長.
的長.
【答案】(![]() )見解析 (
)見解析 (![]() )
)![]() .
.
【解析】(1)連接OB.由切線的性質先證明∠OBE=∠EFB+∠CBO=90°,再由圓周角定理得出∠CBD=∠CBO+∠OBD=90°,故∠EBF=∠OBD,根據等腰三角形的性質可知∠OBD=∠CDB,故∠EBF=∠CDB,進而可得結論;
(2)由(1)可知![]() ∽
∽![]() ∠OBE=90°,∠E=∠C,在Rt△BOE中,利用銳角三角函數的定義即可得出結論.
∠OBE=90°,∠E=∠C,在Rt△BOE中,利用銳角三角函數的定義即可得出結論.
證明:(![]() )∵
)∵![]() ,∴
,∴![]() ,
, ![]() (兩直線平行,內錯角相等,同位角相等).
(兩直線平行,內錯角相等,同位角相等).
連接![]() ,
,
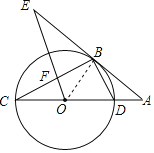
∵過點![]() 的切線
的切線![]() 與
與![]() 的延長線交于點
的延長線交于點![]() ,
,
∴OB⊥AE,
∴∠OBE=∠EFB+∠CBO=90°,
![]() 為⊙
為⊙![]() 的直徑,
的直徑,
∴∠CBD=∠CBO+∠OBD=90°,
∴∠EBF=∠OBD,
∵OB、OD是⊙O的半徑,
∴OB=OD,
∴∠OBD=∠CDB,
∴∠EBF=∠CDB,
∵![]() ,
,
∴∠EFB=∠CBD,
∴![]() ∽
∽![]() .
.
(![]() )由1)可知
)由1)可知![]() ∽
∽![]()
∴∠OBE=90°,
∴∠E=∠C,
∵∠C=30°,
∴∠E=∠C=30°,
∵⊙O的半徑為3,
在Rt△BOE中,∠OBE=90°,∠E =30°,OB=3,
∴![]() ,即
,即![]() ,
,
∴![]() 的長為
的長為![]() .
.


 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案科目:初中數學 來源: 題型:
【題目】在一次課題學習活動中,老師提出了如下問題:如圖,四邊形![]() 是正方形,點
是正方形,點![]() 是邊
是邊![]() 的中點,
的中點,![]() ,且
,且![]() 交正方形外角平分線
交正方形外角平分線![]() 于點
于點![]() .請你探究
.請你探究![]() 與
與![]() 存在怎樣的數量關系,并證明你的結論正確.經過探究,小明得出的結論是
存在怎樣的數量關系,并證明你的結論正確.經過探究,小明得出的結論是![]() ,而要證明結論
,而要證明結論![]() ,就需要證明
,就需要證明![]() 和
和![]() 所在的兩個三角形全等,但
所在的兩個三角形全等,但![]() 和
和![]() 顯然不全等(一個是直角三角形,一個是鈍角三角形),考慮到點
顯然不全等(一個是直角三角形,一個是鈍角三角形),考慮到點![]() 是邊
是邊![]() 的中點,小明想到的方法是如圖2,取
的中點,小明想到的方法是如圖2,取![]() 的中點
的中點![]() ,連接
,連接![]() ,證明
,證明![]() .從而得到
.從而得到![]() .請你參考小明的方法解決下列問題.
.請你參考小明的方法解決下列問題.
(1)如圖3,若把條件“點![]() 是邊
是邊![]() 的中點”改為“點
的中點”改為“點![]() 是邊
是邊![]() 上的任意一點”,其余條件不變,證明結論
上的任意一點”,其余條件不變,證明結論![]() 仍然成立;
仍然成立;
(2)如圖4,若把條件“點![]() 是邊
是邊![]() 的中點”改為:“點
的中點”改為:“點![]() 是邊
是邊![]() 延長線上的一點”,其余條件仍不變,那么結論
延長線上的一點”,其余條件仍不變,那么結論![]() 是否還成立?若成立,請完成證明過程,若不成立,請說明理由.
是否還成立?若成立,請完成證明過程,若不成立,請說明理由.




查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在“愛滿揚州”慈善一日捐活動中,學校團總支為了了解本校學生的捐款情況,隨機抽取了50名學生的捐款數進行了統計,并繪制成統計圖.

(1)這50名同學捐款的眾數為 元,中位數為 元;
(2)求這50名同學捐款的平均數;
(3)該校共有600名學生參與捐款,請估計該校學生的捐款總數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線y=kx-2與坐標軸所圍圖形的面積為3,點A(3,m)是直線y=kx-2上一點.
(1)求點A的坐標;
(2)點P在y軸上,且∠PAO=30°,直接寫出點P坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
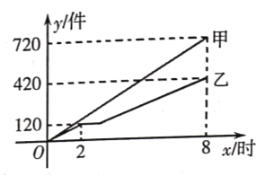
【題目】六一兒童節來臨之際,某服裝廠要加工一批服裝捐贈給貧困山區的孩子們該廠甲、乙兩個車間同時開工趕制這批服裝,從開始加工到加工完這批服裝,甲車間連續工作了![]() 小時,乙車間中途停工一段時間維修設備,修好后按停工前的工作效率繼續加工,直到與甲車間同時完成這批服裝的加工任務為止如圖,是甲、乙兩個車間各自加工的服裝數量
小時,乙車間中途停工一段時間維修設備,修好后按停工前的工作效率繼續加工,直到與甲車間同時完成這批服裝的加工任務為止如圖,是甲、乙兩個車間各自加工的服裝數量![]() (件)與時間
(件)與時間![]() (時)的函數圖象.
(時)的函數圖象.
![]() 甲、乙兩車間一共加工的服裝件數是 件;甲車間每小時加工服裝的件數是 件.
甲、乙兩車間一共加工的服裝件數是 件;甲車間每小時加工服裝的件數是 件.
![]() 乙車間中途停工維修設備用了多長時間?
乙車間中途停工維修設備用了多長時間?
![]() 求乙車間維修設備后,乙車間加工服裝的數量
求乙車間維修設備后,乙車間加工服裝的數量![]() 與
與![]() 之間的函數表達式
之間的函數表達式
![]() 開工后多長時間,甲、乙兩個車間共同完成了
開工后多長時間,甲、乙兩個車間共同完成了![]() 件服裝的加工.
件服裝的加工.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在⊙O中,直徑AB=6,BC是弦,∠ABC=30°,點P在BC上,點Q在⊙O上,且OP⊥PQ.
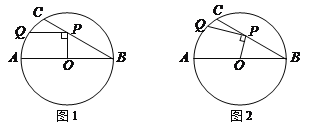
(1)如圖1,當PQ∥AB時,求PQ的長度;
(2)如圖2,當點P在BC上移動時,求PQ長的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
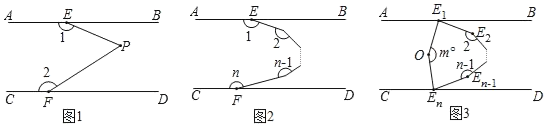
【題目】(提出問題)(1)如圖1,已知AB∥CD,證明:∠1+∠EPF+∠2=360°;
(類比探究)(2)如圖2,已知AB∥CD,設從E點出發的(n﹣1)條折線形成的n個角分別為∠1,∠2……∠n,探索∠1+∠2+∠3+……+∠n的度數可能在1700°至2000°之間嗎?若有可能請求出n的值,若不可能請說明理由.
(拓展延伸)(3)如圖3,已知AB∥CD,∠AE1E2的角平分線E1O與∠CEnEn﹣1的角平分線EnO交于點O,若∠E1OEn=m°.求∠2+∠3+∠4+…+∠(n﹣1)的度數.(用含m、n的代數式表示)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com